Analysis Example of Bayesian MCPMod for Continuous Data

library(BayesianMCPMod)
library(RBesT)
library(clinDR)
library(dplyr)
library(tibble)
library(reactable)

set.seed(7015)

display_params_table <- function(named_list) {
  round_numeric <- function(x, digits = 3) if (is.numeric(x)) round(x, digits) else x
  tbl <- data.frame(
    Name  = names(named_list),
    Value = I(lapply(named_list, function(v) {
      if (inherits(v, "Date")) v <- as.character(v)
      if (!is.null(names(v))) paste0("{", paste(names(v), v, sep="=", collapse=", "), "}")
      else v
    }))
  )
  tbl$Value <- lapply(tbl$Value, round_numeric)
  knitr::kable(tbl)
}

Introduction

This vignette demonstrates the application of the BayesianMCPMod package for analyzing a phase 2 dose-finding trial using the Bayesian MCPMod approach.

A more general overview of the R package was provided with a poster presented during the PSI 2024 Conference.

This package makes use of the future framework for parallel processing, which can be set up for example as follows:

future::plan(future::multisession)

Kindly note that due to overhead in many cases a reduced number of worker nodes is preferable and that for short calculations sequential execution can be faster.

Calculation of a MAP Prior

In a first step, a meta analytic prior will be calculated using historical data from 4 trials with main endpoint Change from baseline in MADRS score after 8 weeks. Please note that only information from the control group will be integrated leading to an informative mixture prior for the control group, while for the active groups a non-informative prior will be specified.

data("metaData")
dataset     <- filter(as.data.frame(metaData), bname == "BRINTELLIX")
histcontrol <- filter(
  dataset,
  dose       == 0,
  primtime   == 8,
  indication == "MAJOR DEPRESSIVE DISORDER",
  protid     != 5)

hist_data   <- data.frame(
  trial = histcontrol$nctno,
  est   = histcontrol$rslt,
  se    = histcontrol$se,
  sd    = histcontrol$sd,
  n     = histcontrol$sampsize)

Here, we suggest a function to construct a list of prior distributions for the different dose groups. This function is adapted to the needs of this example. Other applications may need a different way to construct prior distributions.

getPriorList <- function (
  
  hist_data,
  dose_levels,
  dose_names    = NULL,
  robust_weight = 0.5
  
) {
  
  sd_tot <- with(hist_data, sum(sd * n) / sum(n))
  
  gmap <- RBesT::gMAP(
    formula    = cbind(est, se) ~ 1 | trial,
    weights    = hist_data$n,
    data       = hist_data,
    family     = gaussian,
    beta.prior = cbind(0, 100 * sd_tot),
    tau.dist   = "HalfNormal",
    tau.prior  = cbind(0, sd_tot / 4))
  
  prior_ctr <- RBesT::automixfit(gmap)
  
  if (!is.null(robust_weight)) {
    
    prior_ctr <- suppressMessages(RBesT::robustify(
      priormix = prior_ctr,
      weight   = robust_weight,
      sigma    = sd_tot))
    
  }
  
  prior_trt <- RBesT::mixnorm(
    comp1 = c(w = 1, m = summary(prior_ctr)[1], n = 1),
    sigma = sd_tot,
    param = "mn")
  
  prior_list <- c(list(prior_ctr),
                  rep(x     = list(prior_trt),
                      times = length(dose_levels[-1])))
  
  if (is.null(dose_names)) {
    
    dose_names <- c("Ctr", paste0("DG_", seq_along(dose_levels[-1])))
    
  }
  
  names(prior_list) <- dose_names
  
  return (prior_list)
  
}

With the dose levels to be investigated, the prior distribution can be constructed.

dose_levels <- c(0, 2.5, 5, 10)

set.seed(7015) # re-sets seed only for this example; remove in your analysis script
prior_list  <- getPriorList(
  hist_data     = hist_data,
  dose_levels   = dose_levels,
  robust_weight = 0.3)

getESS(prior_list)

##  Ctr DG_1 DG_2 DG_3 
## 19.7  1.0  1.0  1.0

Dose-Response Model Shapes

Candidate models are specified using the {DoseFinding} package. Models can be parameterized using guesstimates or by directly providing distribution parameters. Note that the linear candidate model does not require parameterization.

Note: The LinLog model is rarely used and not currently supported by BayesianMCPMod.

In the code below, the models are “guesstimated” using the DoseFinding::guesst function. The d option usually takes a single value (a dose level), and the corresponding p for the maximum effect achieved at d.

# Guesstimate estimation
exp_guesst  <- DoseFinding::guesst(
  model = "exponential", 
  d = 5, p = 0.2, Maxd = max(dose_levels)
)
emax_guesst <- DoseFinding::guesst(
  model = "emax",
  d = 2.5, p = 0.9
)
sigEmax_guesst <- DoseFinding::guesst(
  model = "sigEmax",
  d = c(2.5, 5), p = c(0.5, 0.95)
)
logistic_guesst <- DoseFinding::guesst(
  model = "logistic",
  d = c(5, 10), p = c(0.1, 0.85)
)

In some cases, you need to provide more information. For instance, sigEmax requires a pair of d and p values, and exponential requires the specification of the maximum dose for the trial (Maxd).

See the help files for model specifications by typing ?DoseFinding::guesst in your console

Of course, you can also specify the models directly on the parameter scale (without using DoseFinding::guesst).

For example, you can get a betaMod model by specifying delta1 and delta2 parameters (scale is assumed to be 1.2 of the maximum dose), or a quadratic model with the delta2 parameter.

betaMod_params   <- c(delta1 = 1, delta2 = 1)
quadratic_params <- c(delta2 = -0.1)

Now, we can go ahead and create a Mods object, which will be used in the remainder of the vignette.

mods <- DoseFinding::Mods(
  linear      = NULL,
  # guesstimate scale
  exponential = exp_guesst,
  emax        = emax_guesst,
  sigEmax     = sigEmax_guesst,
  logistic    = logistic_guesst,
  # parameter scale
  betaMod     = betaMod_params,
  quadratic   = quadratic_params,
  # Options for all models
  doses       = dose_levels,
  maxEff      = -1,
  placEff     = -12.8
)

plot(mods)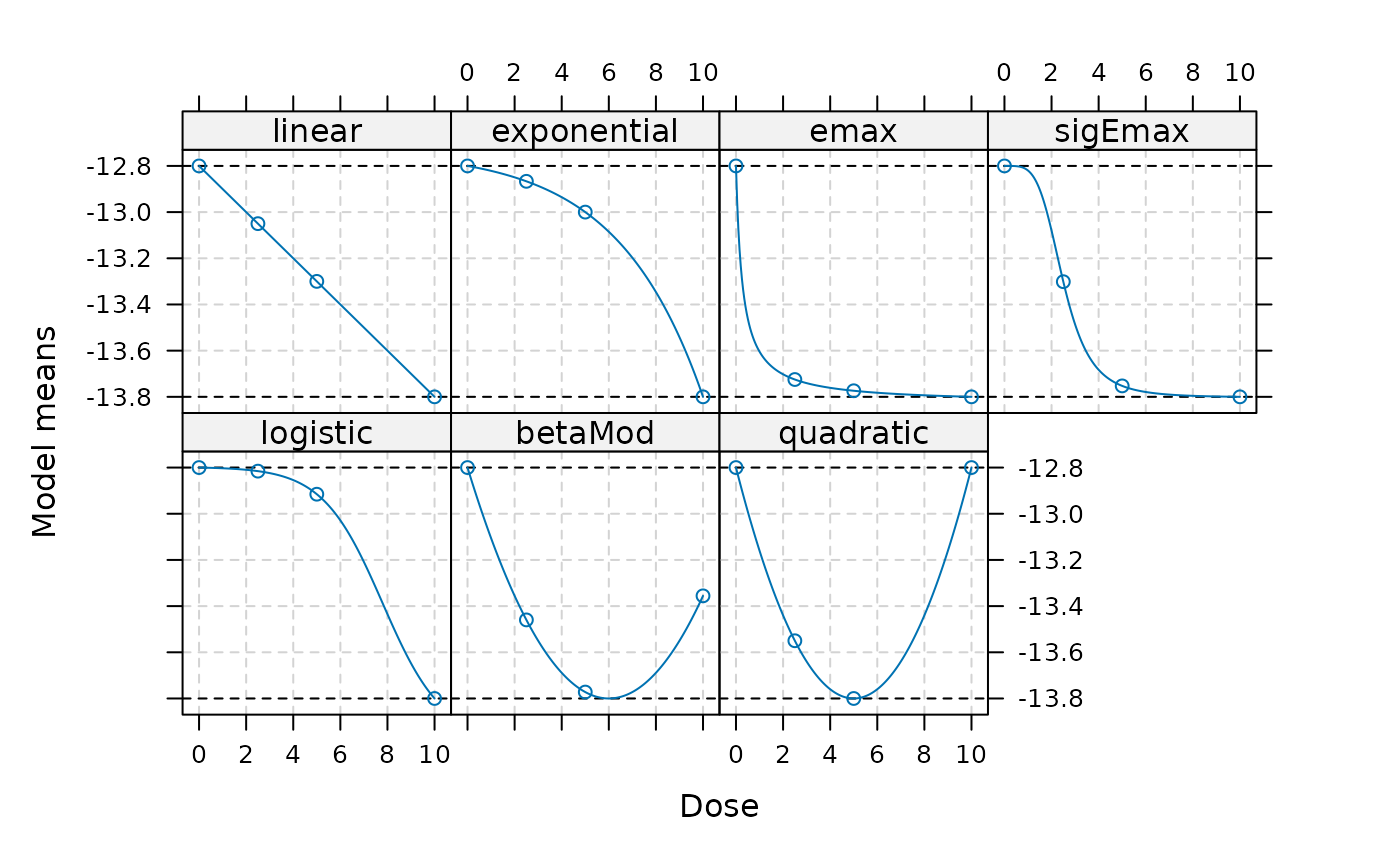

The mods object we just created above contains the full model parameters, which can be helpful for understanding how the guesstimates are translated onto the parameter scale.

display_params_table(mods)

	Name	Value
linear	linear	{e0=-12.8, delta=-0.1}
exponential	exponential	{e0=-12.8, e1=-0.0666665802154335, delta=3.60673602074522}
emax	emax	{e0=-12.8, eMax=-1.02777777777778, ed50=0.277777777777778}
sigEmax	sigEmax	{e0=-12.8, eMax=-1.00277008310249, ed50=2.5, h=4.24792751344358}
logistic	logistic	{e0=-12.7974358974359, eMax=-1.17948717948718, ed50=7.79415312704722, delta=1.27167389072021}
betaMod	betaMod	{e0=-12.8, eMax=-1, delta1=1, delta2=1}
quadratic	quadratic	{e0=-12.8, b1=-0.4, b2=0.04}

And we can see the assumed treatment effects for the specified dose groups below:

knitr::kable(DoseFinding::getResp(mods, doses = dose_levels))

	linear	exponential	emax	sigEmax	logistic	betaMod	quadratic
0	-12.80	-12.80000	-12.80000	-12.80000	-12.80000	-12.80000	-12.80
2.5	-13.05	-12.86667	-13.72500	-13.30138	-12.81551	-13.45972	-13.55
5	-13.30	-13.00000	-13.77368	-13.75263	-12.91538	-13.77222	-13.80
10	-13.80	-13.80000	-13.80000	-13.80000	-13.80000	-13.35556	-12.80

Trial Data

We will use the trial with ct.gov number NCT00735709 as our phase 2 trial data, available in the {clinDR} package (ClinicalTrials.gov 2024).

data("metaData")

trial_data <- dplyr::filter(
  dplyr::filter(tibble::tibble(metaData), bname == "BRINTELLIX"),
  primtime   == 8,
  indication == "MAJOR DEPRESSIVE DISORDER",
  protid     == 5
)

n_patients <- c(128, 124, 129, 122)

Posterior Calculation

In the first step of Bayesian MCPMod, the posterior is calculated by combining the prior information with the estimated results of the trial (Fleischer F 2022).

posterior <- getPosterior(
  prior_list = prior_list,
  mu_hat     = trial_data$rslt,
  S_hat      = diag(trial_data$se^2),
  calc_ess   = TRUE
)

knitr::kable(summary(posterior))

	mean	sd	2.5%	50.0%	97.5%
Ctr	-11.19915	0.7069568	-12.57034	-11.20131	-9.807192
DG_1	-14.88080	0.7130817	-16.27841	-14.88080	-13.483185
DG_2	-15.07981	0.7101057	-16.47159	-15.07981	-13.688031
DG_3	-15.63624	0.7259755	-17.05913	-15.63624	-14.213356

Bayesian MCPMod Test Step

The testing step of Bayesian MCPMod is executed using a critical value on the probability scale and a pseudo-optimal contrast matrix.

The critical value is calculated using (re-estimated) contrasts for frequentist MCPMod to ensure error control when using weakly-informative priors.

A pseudo-optimal contrast matrix is generated based on the variability of the posterior distribution (see (Fleischer F 2022) for more details).

set.seed(7015) # re-sets seed only for this example; remove in your analysis script
crit_pval <- getCritProb(
  mods           = mods,
  dose_levels    = dose_levels,
  cov_new_trial  = diag(trial_data$se^2),
  alpha_crit_val = 0.05
)

contr_mat <- getContr(
  mods          = mods,
  dose_levels   = dose_levels,
  cov_posterior = diag(summary(posterior)[, 2]^2)
)

Please note that there are different ways to derive the contrasts. The following code shows the implementation of some of these ways but it is not executed and the contrast specification above is used.

# i) the frequentist contrast
contr_mat_prior <- getContr(
  mods           = mods,
  dose_levels    = dose_levels,
  dose_weights   = n_patients,
  prior_list     = prior_list)
# ii) re-estimated frequentist contrasts
contr_mat_prior <- getContr(
  mods           = mods,
  dose_levels    = dose_levels,
  cov_new_trial  = diag(trial_data$se^2))
# iii)  Bayesian approach using number of patients for new trial and prior distribution
contr_mat_prior <- getContr(
  mods           = mods,
  dose_levels    = dose_levels,
  dose_weights   = n_patients,
  prior_list     = prior_list)

The Bayesian MCP testing step is then executed:

BMCP_result <- performBayesianMCP(
  posterior_list = posterior,
  contr          = contr_mat, 
  crit_prob_adj  = crit_pval)

Summary information:

BMCP_result

## Bayesian Multiple Comparison Procedure
##   Significant:                   1 
##   Critical Probability:          0.9845439 
##   Maximum Posterior Probability: 0.9999998 
## Posterior Probabilities for Model Shapes
##                        lin       exp      emax      sigE       log     betaM      quad
##   Posterior Prob 0.9999581 0.9981522 0.9999998 0.9999985 0.9953674 0.9999930 0.9883779 
##   Significant            1         1         1         1         1         1         1 
## Average Posterior ESS
##   Dose Level:     Ctr  DG_1  DG_2  DG_3 
##   Avg Post ESS: 189.9 186.6 188.2 180.0

The testing step is significant, indicating a non-flat dose-response shape. All models are significant, with the emax model indicating the greatest deviation from the null hypothesis.

Model Fitting and Visualization

In the model fitting step the posterior distribution is used as basis.

Both simplified and full fitting are performed.

For the simplified fit, the multivariate normal distribution of the control group is approximated and reduced by a one-dimensional normal distribution.

The actual fit (on this approximated posterior distribution) is then performed using generalized least squares criterion. In contrast, for the full fit, the non-linear optimization problem is addressed via the Nelder-Mead algorithm (Wikipedia 2024) implemented by the nloptr package.

The output of the fit includes information about the predicted effects for the included dose levels, the generalized AIC, and the corresponding weights.

For the considered case, the simplified and the full fit are very similar, so we present the full fit.

# If simple = TRUE, uses approx posterior
# Here we use complete posterior distribution
model_fits <- getModelFits(
  models      = mods,
  dose_levels = dose_levels,
  posterior   = posterior,
  simple      = FALSE)

Estimates for dose levels not included in the trial:

display_params_table(stats::predict(model_fits, doses = c(0, 2.5, 4, 5, 7, 10)))

	Name	Value
avgFit	avgFit	-11.292, -14.684, -15.134, -15.315, -15.518, -15.530
betaMod	betaMod	-11.246, -14.787, -15.099, -15.246, -15.450, -15.556
emax	emax	-11.244, -14.805, -15.133, -15.257, -15.407, -15.528
exponential	exponential	-12.586, -13.358, -13.870, -14.233, -15.016, -16.348
linear	linear	-12.403, -13.397, -13.994, -14.391, -15.187, -16.380
logistic	logistic	-11.245, -14.837, -15.273, -15.352, -15.390, -15.395
quadratic	quadratic	-11.474, -14.104, -15.165, -15.658, -16.126, -15.535
sigEmax	sigEmax	-11.243, -14.810, -15.092, -15.217, -15.394, -15.565

Plots of fitted dose-response models and an AIC-based average model:

plot(model_fits)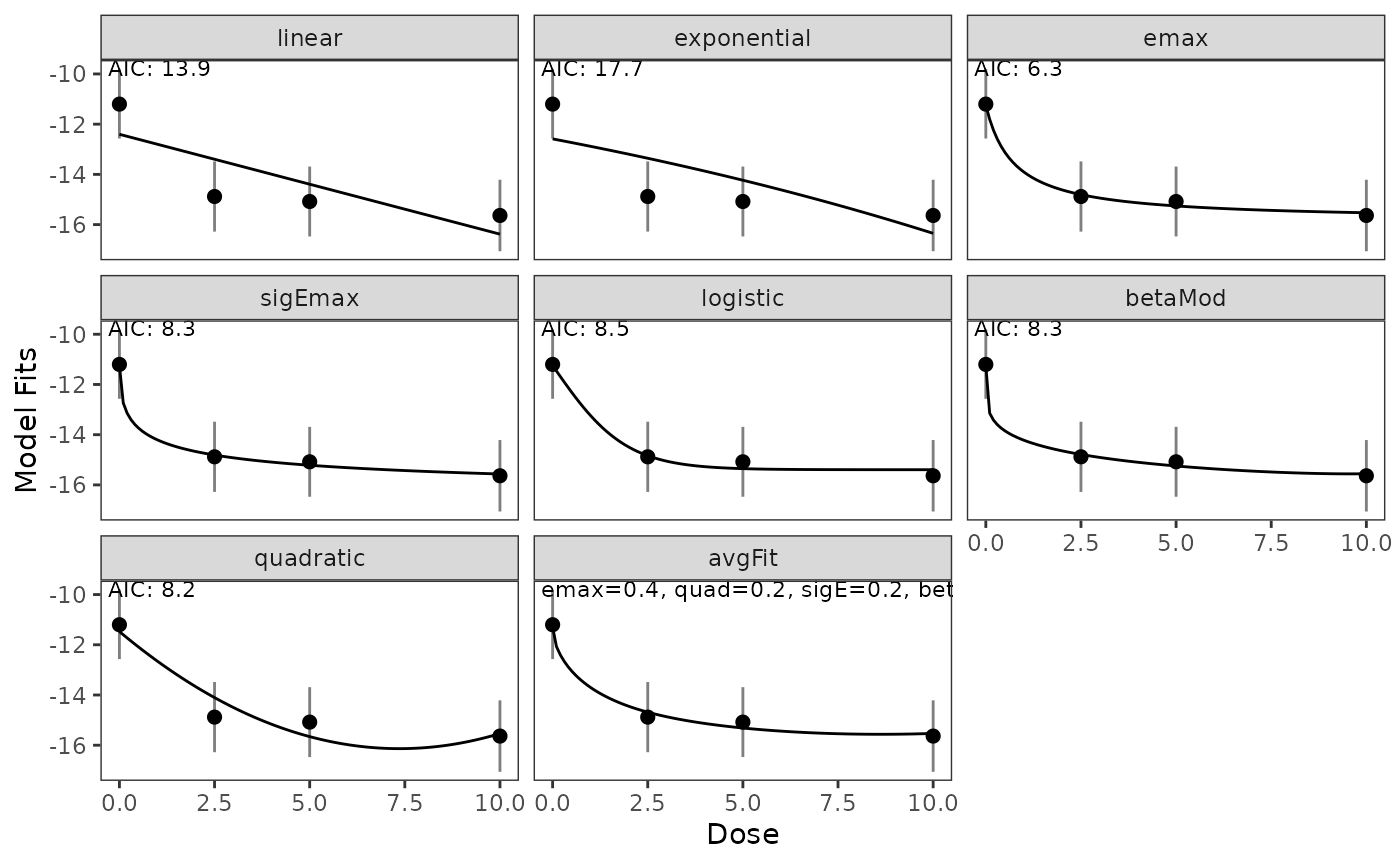

To assess the uncertainty, one can additionally visualize credible bands (orange shaded areas, default levels are 50% and 95%).

These credible bands are calculated with a bootstrap method as follows:

Samples from the posterior distribution are drawn and for every sample the simplified fitting step and a prediction is performed.
These predictions are then used to identify and visualize the specified quantiles.

plot(model_fits, cr_bands = TRUE)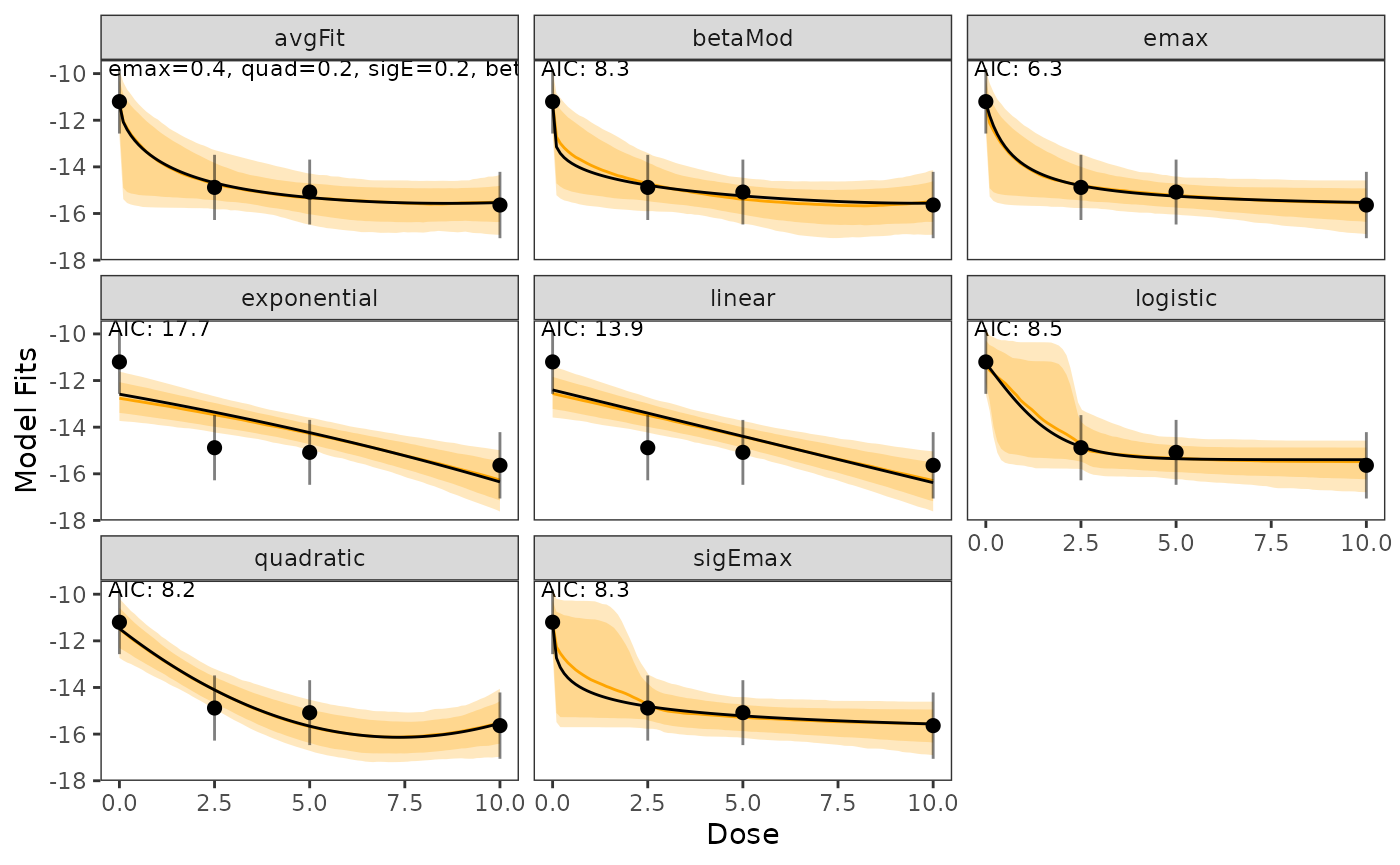

The bootstrap-based quantiles can also be directly calculated via the getBootstrapQuantiles() function and a sample from the model fits can bootstrapped using getBootstrapSamples().

For this example, only 10 samples are bootstrapped for each model fit.

set.seed(7015) # re-sets seed only for this example; remove in your analysis script
bootstrap_quantiles <- getBootstrapQuantiles(
  model_fits = model_fits,
  quantiles  = c(0.025, 0.5, 0.975),
  doses      = c(0, 2.5, 4, 5, 7, 10),
  n_samples  = 10)

The bootstrap quantiles include information about the absolute quantiles (sample_type=abs) and also about the placebo-adjusted (resp. control-adjusted) quantiles (sample_type=diff).

reactable::reactable(
  data = bootstrap_quantiles |>
    tidyr::pivot_wider(names_from = q_prob, values_from = q_val),
  groupBy = "model",
  columns = list(
    dose    = colDef(format = list(aggregated = colFormat(suffix = " dose"))),
    "0.025" = colDef(format = list(cell = colFormat(digits = 4))),
    "0.5"   = colDef(format = list(cell = colFormat(digits = 4))),
    "0.975" = colDef(format = list(cell = colFormat(digits = 4)))
  )
)

Technical note: The median quantile of the bootstrap based procedure is not necessary similar to the main model fit, as they are derived via different procedures.

The main fit (black line) minimizes residuals for the posterior distribution, while the bootstrap median is the median fit of random sampling.

Assessment of the Minimally Efficacious Dose

The Minimally Efficacious Dose (MED) per model shape can be assessed with the function getMED().

getMED(
  delta       = 4,
  model_fits  = model_fits,
  dose_levels = seq(min(dose_levels), max(dose_levels), by = 0.01))

##             avgFit betaMod emax exponential linear logistic quadratic sigEmax
## med_reached   1.00    1.00 1.00           0      0      1.0      1.00    1.00
## med           4.86    5.01 4.88          NA     NA      3.8      4.59    5.25

For an optional Bayesian decision rule for the MED assessment and further details, please see ?getMED().

Additional Note

Testing, modeling, and MED assessment can also be combined via performBayesianMCPMod():

performBayesianMCPMod(
  posterior_list   = posterior,
  contr            = contr_mat,
  crit_prob_adj    = crit_pval,
  delta            = 4,
  simple           = FALSE)

ClinicalTrials.gov. 2024. “NCT00735709.” https://clinicaltrials.gov/study/NCT00735709?term=NCT00735709&rank=1.

Fleischer F, Deng Q, Bossert S. 2022. “Bayesian MCPMod.” Pharmaceutical Statistics 21 (3): 654–70.

Wikipedia. 2024. “Nelder-Mead Method.” https://en.wikipedia.org/wiki/Nelder-Mead_method.

2026-02-19