Evaluate prior specifications of a joint BLRM for oncology dose finding

This vignette illustrates the usage of the decider package for setting up and evaluating prior distributions for joint Bayesian logistic regression model (BLRM)-based dose-finding trials with one or more monotherapy and/or two-compund combination therapy trials that may run sequentially or in parallel. It will be assumed that the reader is familiar with the general process of dose-limiting toxicity (DLT)-based dose-finding trials with the aim of determining a maximum-tolerated dose (MTD) and with the BLRM and its meta-analytic extensions (here referred to as joint BLRM) for DLT-based dose finding. For an introduction to these topics, refer to (Neuenschwander, Branson, and Gsponer 2008), (Neuenschwander et al. 2014), (Neuenschwander, Roychoudhury, and Schmidli 2016). While this terminology and the applied methods mainly originated in the context of oncology dose finding, the methods contained in this vignette can also be applied to other therapeutic areas. Note that different therapeutic areas may be using a slightly different notions instead of e.g. DLT and MTD.

Note further that the term “trial” may also refer to a trial arm (e.g. monotherapy and combination therapy), and that the model will not differentiate between these notions. Moreover, the term “study” will refer to the complete conduct of all jointly modeled trials. That is, simulating e.g. 10 studies means that all involved trials are simulated in the specified order and under the remaining specified assumptions for in total 10 times.

Overview of the main tools

The package ships with two main functions, which are called scenario_jointBLRM and sim_jointBLRM. The former is essentially a high-level wrapper for fitting a joint BLRM to a concrete data scenario, while the latter allows to simulate the course of a number of dose-finding trials under the assumption of a specific dose-toxicity scenario, i.e. a specification of the DLT rates of the involved dose levels.

scenario_jointBLRM

The function scenario_jointBLRM is essentially a wrapper for a Stan model of the joint BLRM, which is internally used to sample from the posterior distribution given a set of input data using the so-called No-U-Turn sampler (NUTS) algorithm. For details on the technicalities behind Stan, a good starting place is Stan’s homepage.

However, besides fitting the model, the function will also perform a number of further evaluations based on the posterior. Most importantly, the posterior distribution of the DLT rates (referred to as posterior toxicities in the following) for a given set of dose levels is determined based on the fitted model. In actual dose-finding trials these distributions will form the basis of the recommended dose level for the next cohort.

The output of scenario_jointBLRM consist of a summary of these posterior toxicities, as well as an evaluation of them in terms of an specific escalation rule. Here, the term escalation rule refers to a method that derives a dosing recommendation based on the fitted BLRM. Currently, the decider package supports the popular escalation with overdose control (EWOC)-based escalation rules (Babb, Rogatko, and Zacks 1998), as well as loss-based escalation rules, which are however not considered in this vignette. Note that EWOC-based escalation is the default setting of all functions, so that without further specifications, the functions will assume that EWOC is applied. Essentially, EWOC computes the probability that the DLT rate of a dose lies above a prespecified target dosing interval (often from 16% to 33% DLT rate), and demands that this probability does not exceed a certain boundary, typically 0.25 (the default). Both the interval and the boundary can be adapted by the user. For EWOC-based escalation, the summary that scenario_jointBLRM creates will contain the resulting posterior interval probabilities of underdosing, target dosing, and overdosing, as well as summary statistics of the posterior of the DLT rates of a given set of doses of interest (which are usually the set of possible dose levels in the trial).

Additionally, plots of the posterior interval probabilities can be created, which visualize the EWOC principle and the set of doses that is allowed by EWOC based on the given data.

The main uses of scenario_jointBLRM are the evaluation of actual and hypothetical data scenarios and the determination of the resulting posterior. Actual data scenarios refer here to data that was observed during a trial, while hypothetical data scenarios are a way of evaluating the on-trial behavior of the BLRM with some escalation rule in a concrete setting. These are particularly important at the planning stage of dose-finding trials, as they allow to monitor the performance of the model in scenarios that are assumed to potentially occur during the trial. Based on these evaluations, the prior distribution of the BLRM can be adapted to obtain appropriate escalation behavior.

For evaluating a prior specification at the planning stage of a trial, one will typically need to consider a whole set of different scenarios that test the model and its recommendation in a broad spectrum of possible situations. Specifically for this setting, the additional function scenario_list_jointBLRM() is provided, which allows to evaluate a list of arbitrarily many scenarios via scenario_jointBLRM() in parallel.

sim_jointBLRM

When a prior with appropriate on-trial behavior is established, one may want to conduct more thorough evaluation of the performance of the resulting model. A widely-accepted way of achieving this are trial simulations. For this, one assumes concrete “true” DLT rates for the dose levels available in a trial (referred to as dose-toxicity scenario) and repeatedly simulates the number of DLTs that are observed in cohorts of patients. Based on this data, the BLRM is fitted and the escalation rule is applied to determine the dose level for the next cohort, or, potentially, if the trial needs to be stopped early (this can e.g. happen when the lowest available dose does not satisfy the EWOC criterion). This process is repeated until a prespecified condition for the declaration of the MTD is reached, or until the trial is stopped without declaring an MTD (either due to stopping early or due to reaching the maximum number of patients that can be enrolled).

Such trial simulation can then be used to determine the operating characteristics of the trial design in specific dose-toxicity scenarios. That is, one simulates a number of trials, e.g. 1000, and determines the ratio of MTDs declared at specific dose levels (e.g., MTDs at target doses), as well as further quantities like the average number of patients treated with a specific dose or the average number of DLTs that occurred during the trial.

This process is then repeated for a number of different scenarios, containing e.g. low-toxicity scenarios (all doses have DLT rate below the targeted interval), moderate scenarios (DLT rates range from underdoses over target doses to overdoses), highly toxic scenarios, and further extreme cases, like e.g. one trial being considerably more toxic than another one.

The function sim_jointBLRM() is designed to perform these simulations in a convenient manner and generate output tables that summarize the operating characteristics of a specified trial design in concrete dose-toxicity scenarios. It provides the option two simulate up to six trials running in parallel (which can be activated independently of each other), namely two monotherapy trials for each involved compound, and two combination therapy trias which are all included in a joint meta-analytic BLRM which is specified according to (Neuenschwander et al. 2014), (Neuenschwander, Roychoudhury, and Schmidli 2016).

The priors used by the model and the order in which cohorts arrive can be freely specified by the user, as well as many further options, including escalation rules, MTD selection, starting doses, and additional restrictions on the increment between escalations. Furthermore, the function allows to include data from arbitrarily many historical trials (not actively simulated) for the involved compounds.

Setting up and evaluating priors using scenario_jointBLRM

Assume in the following that we are interested in setting up an oncology dose-finding study that includes two different trials, referred to as Arm A and Arm B in the following. Suppose that Arm A investigates on some treatment, say compound 1, in a first-in-human monotherapy setting, while Arm B shall consider combination therapy with compound 1 and some combination partner, say compound 2. We assume that previous dose-finding trials for compound 2 were already conducted, so that DLT data is available for monotherapy with compound 2 from earlier clinical investigations.

Assume further that Arm A and Arm B shall run partially in parallel, or, more precisely, that Arm B will be initiated before Arm A has concluded (before the trial declared an MTD), provided that the involved doses of compound 1 were already tested in monotherapy. To allow exchange of information across Arms A and B, and further the inclusion of the historical data for compound 2, we will model both trials and the historical trials in a joint BLRM. The following sections provide an overview how the function scenario_jointBLRM can be set up for this situation, and how it is used to specify and evaluate an appropriate prior distribution and conduct analyses to determine the next dose level during the trial.

Before you continue, do not forget to load the decider package.

library(decider)

Basic specifications of scenario_jointBLRM

As a first step, we will determine the necessary fixed input data, consisting of a set of available dose levels for Arms A ad B, the set of historical data, and reference dose levels for both compounds.

First, assume that from an historical monotherapy trial for compound 2, the clinical data given below is available. Dose levels of the same compound are assumed to be stated in some fixed unit of measurement, e.g. mg or mg/kg, which is not explicitly denoted for simplicity.

Dose	#Patients	#DLT
2	3	0
4	3	0
8	3	0
12	9	1
16	12	2

It is further assumed that all of these observations originate from a single historical trial, although this could easily be extended to multiple historical trials (described below).

The given data now needs to be written in the format that scenario_jointBLRM accepts, which is a named list containing the entries dose1, dose2, n.pat, n.dlt, and trial. For the data given above, use

historical.data = list(
  dose1 = c( 0,    0,    0,    0,    0),
  dose2 = c( 2,    4,    8,    12,   16),
  n.pat = c( 3,    3,    3,    9,    12),
  n.dlt = c( 0,    0,    0,    1,    2),
  trial = c("H1", "H1", "H1", "H1", "H1")
)

Here, each column in the structure given above translates to the data observed at one dose level during a specific historical trial. Note that the dose levels of compound 2 are given in the entry dose2, while the entry of dose1 is 0 to indicate that the cohorts received monotherapy with compound 2.

In the example here, only the data from one historical trial is included. For this, the same entry of historical.data$trial is given for each historical cohort, which tells the function that all of these cohorts belong to the same trial. The entry "H1" is an arbitrarily chosen trial name for the historical trial, note that one could also use a specific number or some other string as trial name. When data for multiple historical trials in given, multiple trial names need to be used to indicate this.

As a next step, we need to specify reference dose levels and the set of available dose levels for the trial. Although the set of investigational dose levels can be flexible in practice (i.e., does not need full specification at the planning stage), for prior evaluations, a hypothetical set of doses that are planned to be used in the trial need to be specified to allow evaluating the hypothetical on-trial behavior of the model.

We will in the following assume that the planned monotherapy doses for compound 1 are

d1 = c(0.1, 0.2, 0.4, 0.8, 1.6, 2.4, 3.6, 5, 6)

where we have again left out the unit of measurement (e.g. g or mg/kg) for simplicity. Regarding combination therapy, suppose that it is planned to consider all combinations of the monotherapy doses of compound 1 with the dose levels

d2 = c(8, 12)

of compound 2 (given in the same unit of measurement as the doses in the historical data).

The planned monotherapy and combination therapy doses should be given to the function via the argument doses.of.interest, which specifies which dose levels need to be evaluated. The argument needs to be a matrix with two rows and one column for each dose level, where monotherapy doses are indicated by placing 0 or NA in the entry of the other compound.

In the setting specified above, this results in

doses.of.interest = rbind( c(d1,                  rep(d1, times=length(d2))),
                           c(rep(0, length(d1)),  rep(d2, each=length(d1))) )

#monotherapy compound 1.
doses.of.interest[, 1:length(d1)]
#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
#> [1,]  0.1  0.2  0.4  0.8  1.6  2.4  3.6    5    6
#> [2,]  0.0  0.0  0.0  0.0  0.0  0.0  0.0    0    0

#combinations of compound 1 with dose 8 of compound 2.
doses.of.interest[, (length(d1)+1):(2*length(d1))]
#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
#> [1,]  0.1  0.2  0.4  0.8  1.6  2.4  3.6    5    6
#> [2,]  8.0  8.0  8.0  8.0  8.0  8.0  8.0    8    8

#combinations of compound 1 with dose 12 of compound 2.
doses.of.interest[, (2*length(d1)+1):(3*length(d1))]
#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
#> [1,]  0.1  0.2  0.4  0.8  1.6  2.4  3.6    5    6
#> [2,] 12.0 12.0 12.0 12.0 12.0 12.0 12.0   12   12

Next, we need to specify the reference doses used by the joint BLRM. We assume that for compound 1 the dose 6 and for compound 2 the dose 12 was selected for this:

dose.ref1 = 6
dose.ref2 = 12

To explicitly tell the function that we are interested in two trials which consider monotherapy for compound 1, respectively combination therapy, we now include the following optional arguments:

trials.of.interest = c("A",     "B")
types.of.interest =  c("mono1", "combi")

The trial names "A" and "B" are arbitrary and tell the function that this is how we will indicate the two trials in the data. The types "mono1" and "combi" specify that only the doses.of.interest for the corresponding trial type need to be analyzed for the corresponding trial. That is, trial "A" is the trial of type "mono1" and will only consider monotherapy with compound 1, while "combi" indicates that trial "B" will only consider combination therapy doses. There is also the type "all" which will cause the function to analyze all given doses of interest for a trial.

If the trials of interest or their type are not explicitly specified, the function will use all trial names given in data and historical data (in our case, including the trial "H1" from the historical data), and further try to infer the type from the given data for this trial. If this is not possible, (e.g. when no data is given yet), the function will provide posteriors for all doses of interest for this trial. Therefore, specifying trials of interest and their types allows to control which output is included in a more precise fashion.

Furthermore, when we do not provide data for trial "A" or "B" yet (e.g. to obtain the predictive distribution induced by the data from the other included trials), the function would not include the posterior of the trial in the output unless its name is specified explicitly as a trial of interest. For instance, when only the historical data is given, the function would only estimate the posterior of the historical trials but not estimate the predictive distribution of a new trial based on the historical data.

At this point, we could in principle already run the function to produce posterior predictive distributions for the trials "A" and "B" purely from the historical data of trial "H1" (which is equivalent to a meta-analytic predictive prior, cf. (Neuenschwander, Roychoudhury, and Schmidli 2016)). However, we still have not specified a (hyper-)prior distribution for the model, so that the function would apply the default prior configuration (refer to the documentation of scenario_jointBLRM). While the default prior is weakly informative and was found to be quite flexible across different situations, it is still recommended to specify a prior manually to ensure good on-trial behavior of the model This will be the subject of the next section.

Specifying a prior for the joint BLRM

Refer to the section Detail in the documentation of scenario_jointBLRM for a model specification of the joint BLRM and explanations what the model does. For the following, it is only important to know that the prior specifications consist of two parts, namely, a prior for the hyper-means (argument prior.mu) and a prior for the between-trial heterogeneities (argument prior.tau), where the hyper-mean is the shared mean of the parameters across trials and the between-trial heterogeneity is the standard deviation across trials. Recall the five different parameters of the joint BLRM: two parameters for each compound (more precisely, the intercept \(log(\alpha_i)\) and the log-slope \(log(\beta_i)\) for compound \(i\)), and the interaction parameter, \(\eta\). Hence, the prior specification must specify the distribution of the hypermean and between-trial heterogeneity for these five parameters.

For this, it is assumed that all hypermeans follow normal distributions with some fixed mean and SD (which are therefore the input required to specify the distribution of each hypermean), while the heterogeneities are assumed to follow log-normal distributions, whose mean and SD (on log-scale) need to be given to the function. Technically, it is further assumed that for each \(i\), \(log(\alpha_i)\) and \(log(\beta_i)\) may be correlated with some correlation coefficient \(\rho\), but this hyperparameter is automatically assigned a uniform distribution on the interval \([-1, 1]\), so that its prior does not need to be specified.

Prior for the hypermeans: prior.mu

First, consider the prior for the hypermeans, which is encoded in the argument prior.mu. This must be a list with five named entries, where each entry provides the mean and SD of the distribution of one of the five hypermeans.

The expected format of this argument is:

#               Parameter    Mean        SD
prior.mu = list(mu_a1  =  c(-0.7081851, 2),
                mu_b1  =  c(0,          1),
                mu_a2  =  c(-0.7081851, 2),
                mu_b2  =  c(0,          1),
                mu_eta =  c(0,          1.121))

Here, the prefix mu indicates that this is a hypermean, while the suffixes correspond to the parameters as given in the following table.

Parameter	Suffix
\(log(\alpha_1)\)	_a1
\(log(\beta_1)\)	_b1
\(log(\alpha_2)\)	_a2
\(log(\beta_2)\)	_b2
\(\eta\)	_eta

In the prior list, each of the entries should be of the form c(x, y), where x gives the mean and y the SD of the normal distribution assumed for the hypermean of the corresponding parameter.

The default values were oriented towards (Neuenschwander et al. 2014) and (Neuenschwander, Roychoudhury, and Schmidli 2016), and represent a relatively flexible, weakly informative prior distribution. It is recommended that this is used as a starting point for adapting the prior to a given setting, as specific modifations to match the setting of a concrete trial will most likely provide better performance than the default prior.

Regarding the interpretation of the parameter, \(log(\alpha_i)\) gives the median log-odds of experiencing a DLT following treatment at the reference dose. The value -0.7081851 corresponds to

logit(0.33)
#> [1] -0.7081851

which means that one assumes the reference dose to have in median a DLT rate of 33%. This corresponds precisely to the upper boundary of the default target interval (from 16% to 33%), so that the prior expresses the assumption that the reference dose is a priori a possible candidate for the MTD (note that the reference dose should be chosen accordingly).

The default value of the SD of the hypermeans of \(log(\alpha_i)\) is 2, which represents a relatively large uncertainty and leads to relatively flexible prior. Note however that depending on the dosing range and other specifications of the trial, one might want to deviate from this default value. For instance, we may want to assume a slightly larger uncertainty regarding the intercept to obtain a more conservative setup, e.g. via

prior.mu = list(mu_a1  =  c(-0.7081851, 3),
                mu_b1  =  c(0,          1),
                mu_a2  =  c(-0.7081851, 3),
                mu_b2  =  c(0,          1),
                mu_eta =  c(0,          1.121))

Regarding the hyperpriors for \(log(\beta)\), a standard normal distribution is assumed. This covers a relatively broad range of slopes, although one may want to select a larger or smaller SD in certain cases. Regarding the mean, it is typically not necessary to deviate from the default of 0 unless there is very concrete information about the shape of the dose-toxicity relationship.

For the interaction parameter, recall that negative values of \(\eta\) express a lower DLT rate of dose combinations than the interaction free-case (in which the compounds would cause DLT fully independently from each other), while positive values lead to a larger DLT rate compared to the interaction-free case. The default value of \(0\) for the mean expresses that both positive and negative interactions may occur, while the SD of 1.121 is selected so that the 95% credible interval of the interaction-parameters corresponds to an increase up to 9-fold (or decrease by factor of 9) of the odds for a DLT at the reference dose. Larger or lower values of mean and SD can be used to obtain more aggressive or conservative behavior of combination trials. Refer e.g. to (Neuenschwander et al. 2014) for more detail on this.

Prior for the between-trial heterogeneities: prior.tau

The prior parameters for the between-trial heterogeneity control the amount of borrowing that is performed across trials. In this context, the assumption of a larger heterogeneity for a parameter allows this parameter to show larger variance across trials, and, consequently, reduces the influence that data from other trials have on each jointly modeled trial.

The decider package assumes that the between-trial heterogeneities follow log-normal distributions, which are specified by providing their mean and SD on log-scale.

The default value and required format of prior.tau is:

#                Parameter    Mean        SD
prior.tau = list(tau_a1  =  c(log(0.25),  log(2)/1.96),
                 tau_b1  =  c(log(0.125), log(2)/1.96),
                 tau_a2  =  c(log(0.25),  log(2)/1.96),
                 tau_b2  =  c(log(0.125), log(2)/1.96),
                 tau_eta =  c(log(0.125), log(2)/1.96))

The naming conventions are the same as for prior.mu.

Note that a value of c(x,y) as tau_[...] provides the mean x and SD y on log-scale, i.e. if the corresponding hyperparameter is denoted as \(\tau\), the function assumes that \(\tau=exp(\psi)\) for some random variable \(\psi\) that is normally distributed with mean x and SD y.

The default values are oriented towards (Neuenschwander et al. 2014). Note that the SDs are typically all set to either log(2)/1.96 or log(4)/1.96 (larger uncertainty), other values are usually not needed.

To specify the mean for the between-trial heterogeneities, one typically assumes a specific degree of heterogeneity (cf. table below). By default, scenario_jointBLRM assumes the mean to be log(0.25) for the between-trial heterogeneity of \(log(\alpha_i)\), and log(0.125) for the heterogeneity of the remaining parameters. On natural (non-log) scale, this means that differences of the parameters across trials are in median expected to be 0.25, respectively 0.125. This is usually referred to as “moderate” between-trial heterogeneity, other potential values for the mean can be found in the following table.

Heterogeneity	\(log(\alpha_i)\)	\(log(\beta_i)\) / \(\eta\)
Small	log(0.125)	log(0.0625)
Moderate	log(0.25)	log(0.125)
Substantial	log(0.5)	log(0.25)
Large	log(1)	log(0.5)

Regarding the prior setup for the between-trial heterogeneity, the chosen prior should depend on the expected differences across trials and the number of patients in the included co-data (larger number of patients may require more heterogeneity to ensure sufficient robustness). For many situations, the moderate and substantial configurations from the above table provide acceptable robustness, so that these are typically considered to be good starting points for prior evaluations. Besides the evaluations of hypothetical scenarios and simulations (covered in the following sections), prior effective sample sizes also provide a good way of evaluating the influence of co-data on the trial of interest and adjusting the priors for the between-trial heterogeneity accordingly. Refer to (Neuenschwander et al. 2020) for more detail on this type of method for assessing the information included in the prior.

Using scenario_jointBLRM to evaluate hypothetical data scenarios

Hypothetical data scenarios evaluate the decisions of the BLRM in a number of concrete situations that might occur in the trial that is planned. While one can usually not foresee and evaluate all possible situations (mostly due to there being too many of them), one restricts these evaluations to important classes of settings. These include but are not limited to:

• Early scenarios that assess the decisions within the first few cohorts of a trial, especially scenarios that assume early DLTs.

• Late scenarios that assess the resulting MTD estimates based on the planned number of patients (or slightly fewer).

• Scenarios that assess specific critical dosing recommendations, e.g. whether the escalation rule ceases to increase the dose when observing certain DLT rates.

• Scenarios that assume heterogeneous co-data. Here, it is e.g. assessed whether the decision rule can correctly decide in settings where the involved trials or trials show substantially different toxicities.

• Similarly to the previous point, if multiple parallel trials are involved that start at different points in time, it should be assessed how the co-data influences the start of the trials. For instance, it can happen that the combination trial is not allowed to be started at the planned starting dose due to toxic monotherapy data. It should therefore be assessed (and aligned with ones recommendations) which co-data is needed to allow the planned starting dose, and in which cases this would not be recommended by the model.

As an example, consider the scenario that the first cohort of 3 patients was treated at the dose 0.1 of compound 1 and a second cohort at the dose 0.2. We assume further that no DLT occurred in the first cohort, while one of the patients of the second cohort experienced DLT. This translates to the data scenario:

scenario1 = list(
  dose1 = c( 0.1,  0.2),
  dose2 = c( 0,    0),
  n.pat = c( 3,    3),
  n.dlt = c( 0,    1),
  trial = c("A",  "A")
)

Note that "A" was used as trial name for the monotherapy trial for compound 1, as this needs to match the name specified in the trials.of.interest argument.

Now, the scenario function can be called. Using the previously specified objects, the function can be applied via

result1 <- scenario_jointBLRM(
  data = scenario1,
  historical.data = historical.data,
  doses.of.interest = doses.of.interest,
  dose.ref1 = dose.ref1,
  dose.ref2 = dose.ref2,
  trials.of.interest = trials.of.interest,
  types.of.interest = types.of.interest,
  prior.mu = prior.mu,
  prior.tau = prior.tau
)

print(result1)
#> $`trial-A`
#>          mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+0 0.11859 0.11397 0.00277 0.08298 0.42437     0.73012        0.20692     0.06296
#> 0.2+0 0.16858 0.14123 0.00622 0.13118 0.52599     0.57770        0.28426     0.13804
#> 0.4+0 0.23990 0.18077 0.01177 0.19979 0.66828     0.41439        0.30802     0.27759
#> 0.8+0 0.32845 0.22607 0.01943 0.28842 0.82258     0.28763        0.27302     0.43935
#> 1.6+0 0.42193 0.26338 0.02855 0.39217 0.92793     0.19970        0.22465     0.57565
#> 2.4+0 0.47413 0.27850 0.03468 0.45659 0.96162     0.16412        0.19714     0.63874
#> 3.6+0 0.52269 0.28863 0.04127 0.52290 0.98040     0.13637        0.17219     0.69144
#> 5+0   0.55892 0.29362 0.04641 0.57564 0.98885     0.11860        0.15342     0.72798
#> 6+0   0.57778 0.29531 0.04980 0.60451 0.99195     0.11001        0.14404     0.74595
#> 
#> $`trial-B`
#>           mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+8  0.18629 0.13531 0.02394 0.15155 0.53989     0.52862        0.33361     0.13777
#> 0.2+8  0.23094 0.15907 0.03199 0.19187 0.63372     0.40750        0.36679     0.22571
#> 0.4+8  0.29299 0.18960 0.04220 0.25081 0.74998     0.28991        0.35425     0.35584
#> 0.8+8  0.37122 0.22352 0.05499 0.33055 0.86179     0.19460        0.30452     0.50088
#> 1.6+8  0.45729 0.25390 0.06750 0.43033 0.94195     0.13229        0.24075     0.62696
#> 2.4+8  0.50649 0.26808 0.07326 0.49341 0.96861     0.11074        0.20394     0.68532
#> 3.6+8  0.55217 0.27991 0.07487 0.55814 0.98426     0.09771        0.17248     0.72981
#> 5+8    0.58535 0.28891 0.07207 0.61212 0.99170     0.09375        0.15140     0.75485
#> 6+8    0.60188 0.29425 0.06797 0.64102 0.99437     0.09407        0.14083     0.76510
#> 0.1+12 0.22163 0.13567 0.04560 0.19111 0.56602     0.39149        0.42356     0.18495
#> 0.2+12 0.26436 0.15705 0.05503 0.23029 0.65521     0.29229        0.42656     0.28115
#> 0.4+12 0.32378 0.18514 0.06661 0.28640 0.76281     0.20083        0.38479     0.41438
#> 0.8+12 0.39874 0.21714 0.07997 0.36279 0.86979     0.13339        0.31136     0.55525
#> 1.6+12 0.48109 0.24729 0.09018 0.45862 0.94615     0.09510        0.23439     0.67051
#> 2.4+12 0.52780 0.26299 0.09012 0.52017 0.97151     0.08508        0.19534     0.71958
#> 3.6+12 0.57027 0.27851 0.08220 0.58428 0.98658     0.08529        0.16244     0.75227
#> 5+12   0.59971 0.29270 0.06724 0.63718 0.99349     0.09417        0.14046     0.76537
#> 6+12   0.61346 0.30184 0.05647 0.66692 0.99585     0.10270        0.12933     0.76797

Note that the output contains two entries, one for each trial of interest. As we previously specified the types of these trials, the posterior toxicities of trial "A" are only computed for the doses of interest that represent monotherapy with compound 1, while the posteriors for trial "B" only contain the combination therapy dose levels.

For each of these doses, the interval probabilities are computed, as well as summary statistics of the posterior toxicities. By default, the considered interval probabilities assume a target interval (range of DLT rates considered to be appropriate as MTD) of \([0.16, 0.33)\). However, if one is interested in some different interval, say, \([0.2, 0.3)\), this can be achieved by supplying the optional argument dosing.intervals = c(0.2, 0.3). In this context, the underdosing, respectively overdosing intervals contain the DLT rates below, respectively above the target interval.

Further customization of the output can be achieved by supplying the argument probs, which specifies the quantiles listed in the output tables. By default, the reported quantiles are 2.5%, 50%, and 97.5%. If additional quantiles shall be computed, say, 25% and 75%, this can be achieved e.g. with probs = c(0.025, 0.25, 0.5, 0.75, 0.975).

If additional output plots shall be created (not required for prior evaluation, but potentially helpful for actual analyses), one can activate this via plot.decisions = TRUE. Usually, simple bar plots are created by this argument for monotherapy, and a heatmap for combination therapy. By additionally setting plot.return = TRUE, the plots will be contained in the results list in the form of ggplot objects. Refer to the documentation of the ggplot2 package for detail on this type of object. The ggplot2 package also provides a broad range of functions that can be used to customize the returned plots further. If plot.return is not specified, the function will only print the plots and potentially save them if the user specified a path for outputs. Additionally, one may want to control the number of digits the output is rounded to, especially when considering heatmap-type plots for combination therapy, using e.g. digits = 3.

result1a <- scenario_jointBLRM(
  data = scenario1,
  historical.data = historical.data,
  doses.of.interest = doses.of.interest,
  dose.ref1 = dose.ref1,
  dose.ref2 = dose.ref2,
  trials.of.interest = trials.of.interest,
  types.of.interest = types.of.interest,
  prior.mu = prior.mu,
  prior.tau = prior.tau,
  plot.decisions = TRUE,
  plot.return = TRUE,
  ewoc.threshold = 0.25,
  digits = 3
)

The generated plots are shown in the plot panel in RStudio. To explicitly display the returned ggplot objects, one can access them as follows.

plot(result1a$plots$"trial-A")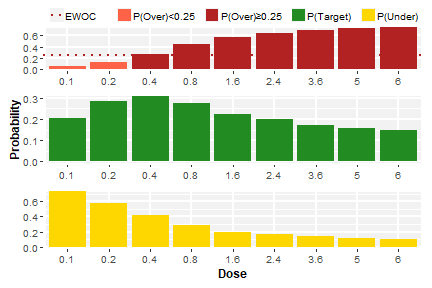

Plot generated by scenario_jointBLRM() for trial "A"

plot(result1a$plots$"trial-B")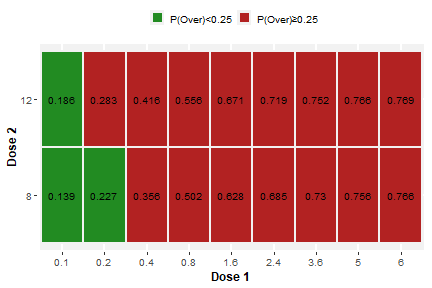

Plot generated by scenario_jointBLRM() for trial "B"

Note that we supplied an additional argument, ewoc.threshold, to the call to scenario_jointBLRM. This argument states the feasibility bound of the EWOC criterion (cf. Babb et al. (1998)) and is displayed by the plots to indicate which doses are fulfilling the EWOC criterion (and could be used for the next cohort). This argument is optional and defaults to 0.25 if not specified, so that it is actually not needed unless a different value shall be used as feasibility bound of the EWOC criterion.

There are further options for customizing plots, e.g. to indicate which type of plots is used for combination therapy trials (heatmap or bar diagram). Detail on this and further arguments for the output plots are specified in the documentation.

One can also enable automatic saving of the posterior summaries by supplying the optional arguments file.name and path. If the latter specifies a valid (writable) directory, the output will be saved as .xlsx file under the specified file.name. Additionally, one can save the output plots by further specifying plots.save = TRUE (provided a valid path and file.name were supplied). In this case, it is recommended to specify the format of the output plots via plot.unit, plot.width, and plot.height. Refer to the documentation for detail on this.

Evaluating multiple scenarios in parallel

When setting up a prior, one will typically want to evaluate a number of scenarios at once, but, as Bayesian computation tends to take relatively long, this may be rather slow for e.g. 10 or more scenarios. Additionally, one would need e.g. 10 (or more) calls to scenario_jointBLRM, which may not be practical if the same scenarios are repeatedly evaluated for slightly altered prior specifications.

To provide slightly more convenience for these types of exercise, the function scenario_list_jointBLRM allows to perform multiple calls to scenario_jointBLRM in parallel for a list of data scenarios, which both speeds up the computation and simplifies the evaluation of a number of hypothetical settings. Please note that a parallel backend needs to be registered to leverage the parallelization, otherwise the function will be executed sequentially. An example is provided below.

To use this, consider first a (numbered) list of data scenarios. This is specified as a list of lists, where each sublist must be of the format expected by the data argument of scenario_jointBLRM. For instance, a list with 8 scenarios could look like this:

data.list = list(

  #Scenario 1
  list(
    dose1 = c( 0.1),
    dose2 = c( 0),
    n.pat = c( 3),
    n.dlt = c( 0),
    trial = c("A")),

  #Scenario 2
  list(
    dose1 = c( 0.1),
    dose2 = c( 0),
    n.pat = c( 3),
    n.dlt = c( 1),
    trial = c("A")),

  #Scenario 3
  list(
    dose1 = c( 0.1),
    dose2 = c( 0),
    n.pat = c( 3),
    n.dlt = c( 2),
    trial = c("A")),

  #Scenario 4
  list(
    dose1 = c( 0.1,  0.2),
    dose2 = c( 0,    0),
    n.pat = c( 3,    3),
    n.dlt = c( 0,    1),
    trial = c("A",  "A")),

  #Scenario 5
  list(
    dose1 = c( 0.1,  0.2),
    dose2 = c( 0,    0),
    n.pat = c( 3,    3),
    n.dlt = c( 0,    2),
    trial = c("A",  "A")),

  #Scenario 6
  list(
    dose1 = c( 0.1,  0.2,  0.4),
    dose2 = c( 0,    0,    0),
    n.pat = c( 3,    3,    3),
    n.dlt = c( 0,    0,    1),
    trial = c("A",  "A",  "A")),

  #Scenario 7
  list(
    dose1 = c( 0.1,  0.2,  0.4),
    dose2 = c( 0,    0,    0),
    n.pat = c( 3,    3,    6),
    n.dlt = c( 0,    0,    1),
    trial = c("A",  "A",  "A")),

  #Scenario 8
  list(
    dose1 = c( 0.1,  0.2,  0.4,     0.2),
    dose2 = c( 0,    0,    0,       8),
    n.pat = c( 3,    3,    6,       3),
    n.dlt = c( 0,    0,    1,       0),
    trial = c("A",  "A",  "A",     "B"))
)

Note that Scenario 8 also contains cohorts from the combination therapy trial, encoded with the trial name "B" as specified previously. The cohorts can be given in arbitrary order.

To run the evaluations in parallel, one can additionally register a paralell backend. There are various existing packages than can achieve this. A basic construct to register a parallel backend using the doFuture package is the following

library(doFuture)

#specify number of cores -- here, only 1 for a sequential exacution
n.cores <- 1

#register backend for parallel execution and plan multisession
doFuture::registerDoFuture()
future::plan(future::multisession, workers=n.cores)

In this example, only 1 core is selected, which is identical to a sequential execution. In practice, n.cores can be set depending on the available processor on which the function is running.

Now, coming back to the evaluation of scenarios, after registration of the parallel backend one can simply use

results <- scenario_list_jointBLRM(
  data.list = data.list,

  historical.data = historical.data,
  doses.of.interest = doses.of.interest,
  dose.ref1 = dose.ref1,
  dose.ref2 = dose.ref2,
  trials.of.interest = trials.of.interest,
  types.of.interest = types.of.interest,
  prior.mu = prior.mu,
  prior.tau = prior.tau
)

print(results)
#> [[1]]
#> [[1]]$`trial-A`
#>          mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+0 0.02629 0.06901 0.00000 0.00108 0.24157     0.95389        0.03335     0.01276
#> 0.2+0 0.03834 0.09010 0.00000 0.00245 0.32889     0.92537        0.04987     0.02476
#> 0.4+0 0.05776 0.12113 0.00000 0.00562 0.45832     0.88396        0.06689     0.04915
#> 0.8+0 0.08879 0.16322 0.00000 0.01303 0.62015     0.82253        0.08784     0.08963
#> 1.6+0 0.13789 0.21527 0.00000 0.03152 0.79474     0.73684        0.10943     0.15373
#> 2.4+0 0.17913 0.24919 0.00004 0.05380 0.87765     0.67021        0.12268     0.20711
#> 3.6+0 0.23398 0.28456 0.00024 0.09469 0.93795     0.58855        0.13350     0.27795
#> 5+0   0.29191 0.31325 0.00068 0.15226 0.96966     0.50889        0.13965     0.35146
#> 6+0   0.33007 0.32909 0.00101 0.19635 0.98156     0.46268        0.14039     0.39693
#> 
#> [[1]]$`trial-B`
#>           mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+8  0.09596 0.09113 0.00620 0.07103 0.34521     0.84208        0.12950     0.02842
#> 0.2+8  0.10744 0.10718 0.00681 0.07642 0.41522     0.80799        0.14739     0.04462
#> 0.4+8  0.12558 0.13146 0.00777 0.08460 0.52825     0.76176        0.16513     0.07311
#> 0.8+8  0.15440 0.16589 0.00922 0.09715 0.67305     0.69641        0.18429     0.11930
#> 1.6+8  0.20040 0.21082 0.01139 0.11942 0.82493     0.60701        0.20309     0.18990
#> 2.4+8  0.23946 0.24139 0.01301 0.14203 0.89541     0.53991        0.21173     0.24836
#> 3.6+8  0.29194 0.27425 0.01475 0.18147 0.94769     0.46073        0.21295     0.32632
#> 5+8    0.34776 0.30211 0.01600 0.23634 0.97595     0.38990        0.20507     0.40503
#> 6+8    0.38430 0.31780 0.01583 0.28020 0.98621     0.35231        0.19340     0.45429
#> 0.1+12 0.13536 0.09759 0.02351 0.11183 0.39383     0.70603        0.24972     0.04425
#> 0.2+12 0.14637 0.11139 0.02459 0.11774 0.45308     0.67355        0.26217     0.06428
#> 0.4+12 0.16381 0.13303 0.02590 0.12662 0.55511     0.62862        0.27497     0.09641
#> 0.8+12 0.19172 0.16481 0.02752 0.14010 0.69082     0.56756        0.28587     0.14657
#> 1.6+12 0.23685 0.20790 0.02896 0.16430 0.83609     0.48787        0.28715     0.22498
#> 2.4+12 0.27570 0.23836 0.02865 0.18959 0.90570     0.43039        0.27716     0.29245
#> 3.6+12 0.32825 0.27247 0.02611 0.23329 0.95521     0.36841        0.25258     0.37901
#> 5+12   0.38362 0.30255 0.02177 0.29273 0.98051     0.32100        0.21730     0.46170
#> 6+12   0.41912 0.31983 0.01832 0.33906 0.98942     0.29912        0.19269     0.50819
#> 
#> 
#> [[2]]
#> [[2]]$`trial-A`
#>          mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+0 0.26814 0.20897 0.00921 0.21871 0.75773     0.39043        0.27542     0.33415
#> 0.2+0 0.33265 0.22806 0.01631 0.29563 0.81783     0.28592        0.26153     0.45255
#> 0.4+0 0.40530 0.24731 0.02576 0.38520 0.87830     0.20253        0.22777     0.56970
#> 0.8+0 0.47981 0.26293 0.03805 0.48000 0.93033     0.14415        0.18695     0.66890
#> 1.6+0 0.55030 0.27216 0.05140 0.57280 0.96564     0.10492        0.14716     0.74792
#> 2.4+0 0.58816 0.27448 0.06003 0.62448 0.97871     0.08794        0.12830     0.78376
#> 3.6+0 0.62306 0.27480 0.06955 0.67288 0.98712     0.07452        0.11243     0.81305
#> 5+0   0.64911 0.27379 0.07744 0.70944 0.99158     0.06503        0.10179     0.83318
#> 6+0   0.66271 0.27281 0.08181 0.72818 0.99340     0.06048        0.09647     0.84305
#> 
#> [[2]]$`trial-B`
#>           mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+8  0.31803 0.21200 0.03883 0.27016 0.80618     0.27978        0.31595     0.40427
#> 0.2+8  0.37464 0.22757 0.04989 0.33596 0.85582     0.20259        0.28851     0.50890
#> 0.4+8  0.43947 0.24221 0.06374 0.41743 0.90237     0.14130        0.24416     0.61454
#> 0.8+8  0.50804 0.25388 0.07906 0.50597 0.94239     0.09733        0.19520     0.70747
#> 1.6+8  0.57453 0.26152 0.09346 0.59612 0.97093     0.07000        0.15119     0.77881
#> 2.4+8  0.61022 0.26465 0.09964 0.64633 0.98202     0.06004        0.13095     0.80901
#> 3.6+8  0.64223 0.26795 0.10260 0.69411 0.98938     0.05503        0.11411     0.83086
#> 5+8    0.66457 0.27211 0.09871 0.73061 0.99358     0.05467        0.10394     0.84139
#> 6+8    0.67519 0.27561 0.09326 0.74971 0.99529     0.05674        0.09900     0.84426
#> 0.1+12 0.34760 0.20579 0.06406 0.30474 0.81568     0.19935        0.34391     0.45674
#> 0.2+12 0.40176 0.22017 0.07626 0.36739 0.86299     0.14068        0.29892     0.56040
#> 0.4+12 0.46378 0.23381 0.09166 0.44455 0.90747     0.09630        0.24390     0.65980
#> 0.8+12 0.52930 0.24507 0.10814 0.52884 0.94589     0.06590        0.18934     0.74476
#> 1.6+12 0.59243 0.25375 0.11766 0.61408 0.97316     0.04924        0.14498     0.80578
#> 2.4+12 0.62561 0.25906 0.11782 0.66298 0.98376     0.04668        0.12468     0.82864
#> 3.6+12 0.65406 0.26685 0.10897 0.70973 0.99105     0.04985        0.11017     0.83998
#> 5+12   0.67204 0.27716 0.09146 0.74623 0.99504     0.05885        0.10170     0.83945
#> 6+12   0.67941 0.28518 0.07847 0.76665 0.99662     0.06699        0.09851     0.83450
#> 
#> 
#> [[3]]
#> [[3]]$`trial-A`
#>          mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+0 0.55392 0.23487 0.10672 0.56626 0.94450     0.05423        0.14813     0.79764
#> 0.2+0 0.62100 0.22417 0.15080 0.65006 0.95843     0.02823        0.09791     0.87386
#> 0.4+0 0.68267 0.21360 0.19681 0.72473 0.97135     0.01569        0.06323     0.92108
#> 0.8+0 0.73574 0.20305 0.24131 0.78820 0.98240     0.00966        0.04240     0.94794
#> 1.6+0 0.77960 0.19223 0.28604 0.83776 0.99039     0.00650        0.02952     0.96398
#> 2.4+0 0.80132 0.18580 0.30996 0.86165 0.99352     0.00502        0.02416     0.97082
#> 3.6+0 0.82049 0.17938 0.33431 0.88245 0.99573     0.00419        0.02007     0.97574
#> 5+0   0.83435 0.17421 0.35317 0.89696 0.99698     0.00354        0.01748     0.97898
#> 6+0   0.84146 0.17137 0.36365 0.90436 0.99751     0.00331        0.01605     0.98064
#> 
#> [[3]]$`trial-B`
#>           mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+8  0.57010 0.23870 0.11961 0.58521 0.95411     0.04638        0.14664     0.80698
#> 0.2+8  0.63093 0.22772 0.16315 0.66154 0.96590     0.02378        0.10065     0.87557
#> 0.4+8  0.68930 0.21501 0.20934 0.73289 0.97661     0.01234        0.06433     0.92333
#> 0.8+8  0.74132 0.20229 0.25455 0.79378 0.98518     0.00676        0.04188     0.95136
#> 1.6+8  0.78449 0.19122 0.29550 0.84357 0.99171     0.00438        0.02938     0.96624
#> 2.4+8  0.80505 0.18657 0.31334 0.86802 0.99443     0.00392        0.02481     0.97127
#> 3.6+8  0.82157 0.18479 0.32088 0.88878 0.99649     0.00436        0.02253     0.97311
#> 5+8    0.83121 0.18717 0.31122 0.90422 0.99773     0.00536        0.02350     0.97114
#> 6+8    0.83470 0.19080 0.29669 0.91165 0.99826     0.00665        0.02486     0.96849
#> 0.1+12 0.58885 0.22947 0.15101 0.60400 0.95623     0.02908        0.13299     0.83793
#> 0.2+12 0.64701 0.21878 0.19374 0.67685 0.96746     0.01465        0.08733     0.89802
#> 0.4+12 0.70278 0.20659 0.23872 0.74507 0.97759     0.00718        0.05475     0.93807
#> 0.8+12 0.75226 0.19485 0.28069 0.80306 0.98590     0.00414        0.03481     0.96105
#> 1.6+12 0.79252 0.18624 0.31502 0.85126 0.99229     0.00310        0.02563     0.97127
#> 2.4+12 0.81058 0.18486 0.32065 0.87471 0.99499     0.00347        0.02347     0.97306
#> 3.6+12 0.82312 0.18922 0.30377 0.89506 0.99708     0.00524        0.02505     0.96971
#> 5+12   0.82759 0.19985 0.26604 0.90954 0.99824     0.00897        0.02914     0.96189
#> 6+12   0.82713 0.20955 0.23260 0.91701 0.99876     0.01278        0.03287     0.95435
#> 
#> 
#> [[4]]
#> [[4]]$`trial-A`
#>          mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+0 0.11867 0.11368 0.00285 0.08317 0.42156     0.72987        0.20847     0.06166
#> 0.2+0 0.16832 0.14058 0.00634 0.13091 0.52177     0.57767        0.28551     0.13682
#> 0.4+0 0.23900 0.17944 0.01193 0.19939 0.66692     0.41518        0.30962     0.27520
#> 0.8+0 0.32700 0.22415 0.01969 0.28785 0.82070     0.28735        0.27547     0.43718
#> 1.6+0 0.42030 0.26144 0.02924 0.39036 0.92652     0.19896        0.22597     0.57507
#> 2.4+0 0.47251 0.27665 0.03573 0.45497 0.96065     0.16300        0.19858     0.63842
#> 3.6+0 0.52117 0.28686 0.04252 0.52053 0.97972     0.13457        0.17341     0.69202
#> 5+0   0.55754 0.29191 0.04842 0.57293 0.98840     0.11601        0.15508     0.72891
#> 6+0   0.57648 0.29364 0.05186 0.60143 0.99151     0.10739        0.14621     0.74640
#> 
#> [[4]]$`trial-B`
#>           mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+8  0.18628 0.13471 0.02386 0.15218 0.53638     0.52684        0.33541     0.13775
#> 0.2+8  0.23069 0.15834 0.03157 0.19210 0.63125     0.40788        0.36582     0.22630
#> 0.4+8  0.29222 0.18850 0.04234 0.24976 0.74582     0.28848        0.35725     0.35427
#> 0.8+8  0.36998 0.22202 0.05526 0.32964 0.85779     0.19335        0.30722     0.49943
#> 1.6+8  0.45580 0.25243 0.06800 0.42798 0.93786     0.13186        0.24138     0.62676
#> 2.4+8  0.50490 0.26668 0.07340 0.49072 0.96565     0.11014        0.20534     0.68452
#> 3.6+8  0.55053 0.27857 0.07551 0.55580 0.98266     0.09668        0.17413     0.72919
#> 5+8    0.58374 0.28762 0.07251 0.60975 0.99057     0.09245        0.15219     0.75536
#> 6+8    0.60032 0.29299 0.06827 0.63837 0.99357     0.09346        0.14078     0.76576
#> 0.1+12 0.22155 0.13495 0.04615 0.19109 0.56234     0.38986        0.42474     0.18540
#> 0.2+12 0.26404 0.15625 0.05524 0.22990 0.65119     0.29205        0.42655     0.28140
#> 0.4+12 0.32295 0.18402 0.06725 0.28584 0.75831     0.19990        0.38786     0.41224
#> 0.8+12 0.39743 0.21564 0.08076 0.36222 0.86533     0.13197        0.31501     0.55302
#> 1.6+12 0.47953 0.24583 0.09131 0.45613 0.94205     0.09378        0.23702     0.66920
#> 2.4+12 0.52616 0.26162 0.09122 0.51759 0.96925     0.08418        0.19670     0.71912
#> 3.6+12 0.56861 0.27725 0.08313 0.58244 0.98505     0.08485        0.16344     0.75171
#> 5+12   0.59812 0.29156 0.06918 0.63659 0.99265     0.09321        0.14154     0.76525
#> 6+12   0.61195 0.30077 0.05775 0.66487 0.99528     0.10149        0.13108     0.76743
#> 
#> 
#> [[5]]
#> [[5]]$`trial-A`
#>          mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+0 0.24977 0.15939 0.02780 0.22110 0.62143     0.34596        0.37606     0.27798
#> 0.2+0 0.33372 0.17764 0.05234 0.31479 0.71227     0.18186        0.34897     0.46917
#> 0.4+0 0.43305 0.20155 0.08178 0.42542 0.82251     0.09285        0.24353     0.66362
#> 0.8+0 0.53212 0.22284 0.11275 0.53840 0.91761     0.05181        0.16035     0.78784
#> 1.6+0 0.61830 0.23384 0.14357 0.64406 0.96940     0.03166        0.10776     0.86058
#> 2.4+0 0.66103 0.23540 0.16184 0.69932 0.98398     0.02440        0.08762     0.88798
#> 3.6+0 0.69831 0.23419 0.17950 0.74859 0.99171     0.01909        0.07211     0.90880
#> 5+0   0.72486 0.23168 0.19371 0.78465 0.99524     0.01579        0.06265     0.92156
#> 6+0   0.73833 0.22983 0.20204 0.80272 0.99649     0.01458        0.05739     0.92803
#> 
#> [[5]]$`trial-B`
#>           mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+8  0.30531 0.17914 0.05170 0.27246 0.72103     0.23654        0.37864     0.38482
#> 0.2+8  0.37687 0.19477 0.07589 0.35207 0.79578     0.13470        0.32380     0.54150
#> 0.4+8  0.46261 0.20991 0.10754 0.45071 0.87398     0.06770        0.23520     0.69710
#> 0.8+8  0.55273 0.22218 0.14098 0.55828 0.93669     0.03485        0.15359     0.81156
#> 1.6+8  0.63459 0.22940 0.17217 0.66147 0.97464     0.02033        0.10184     0.87783
#> 2.4+8  0.67517 0.23175 0.18515 0.71663 0.98638     0.01719        0.08428     0.89853
#> 3.6+8  0.70923 0.23440 0.19008 0.76608 0.99316     0.01686        0.07215     0.91099
#> 5+8    0.73142 0.23858 0.18203 0.80303 0.99632     0.01876        0.06757     0.91367
#> 6+8    0.74133 0.24245 0.17331 0.82163 0.99746     0.02162        0.06618     0.91220
#> 0.1+12 0.33556 0.17496 0.07780 0.30647 0.73527     0.15761        0.39127     0.45112
#> 0.2+12 0.40400 0.18910 0.10365 0.38218 0.80682     0.08480        0.31265     0.60255
#> 0.4+12 0.48600 0.20300 0.13593 0.47605 0.88037     0.04084        0.21272     0.74644
#> 0.8+12 0.57204 0.21483 0.16929 0.57851 0.94061     0.02066        0.13542     0.84392
#> 1.6+12 0.64954 0.22356 0.19358 0.67816 0.97648     0.01398        0.09136     0.89466
#> 2.4+12 0.68696 0.22877 0.19789 0.73125 0.98777     0.01420        0.07767     0.90813
#> 3.6+12 0.71663 0.23699 0.18356 0.78005 0.99423     0.01835        0.07137     0.91028
#> 5+12   0.73360 0.24843 0.15551 0.81524 0.99711     0.02646        0.07069     0.90285
#> 6+12   0.73972 0.25748 0.13210 0.83393 0.99815     0.03410        0.07095     0.89495
#> 
#> 
#> [[6]]
#> [[6]]$`trial-A`
#>          mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+0 0.05911 0.06818 0.00063 0.03493 0.24966     0.91423        0.07783     0.00794
#> 0.2+0 0.09033 0.08776 0.00215 0.06284 0.32539     0.82261        0.15384     0.02355
#> 0.4+0 0.14489 0.12307 0.00565 0.11133 0.45913     0.64384        0.26451     0.09165
#> 0.8+0 0.23176 0.18129 0.01172 0.18675 0.67629     0.43971        0.30121     0.25908
#> 1.6+0 0.34174 0.24353 0.01977 0.29132 0.87424     0.28997        0.26181     0.44822
#> 2.4+0 0.40748 0.27144 0.02508 0.36426 0.94082     0.23060        0.22948     0.53992
#> 3.6+0 0.46949 0.29098 0.03067 0.44250 0.97390     0.18543        0.19892     0.61565
#> 5+0   0.51563 0.30114 0.03564 0.50778 0.98694     0.15717        0.17738     0.66545
#> 6+0   0.53948 0.30490 0.03865 0.54403 0.99138     0.14457        0.16604     0.68939
#> 
#> [[6]]$`trial-B`
#>           mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+8  0.13106 0.09683 0.01567 0.10728 0.37996     0.70805        0.24788     0.04407
#> 0.2+8  0.16116 0.11591 0.02119 0.13268 0.46257     0.60029        0.31297     0.08674
#> 0.4+8  0.21043 0.14603 0.02984 0.17527 0.58846     0.45174        0.36967     0.17859
#> 0.8+8  0.28621 0.18952 0.04152 0.24147 0.75561     0.30389        0.35784     0.33827
#> 1.6+8  0.38493 0.23782 0.05464 0.33850 0.90060     0.19503        0.29274     0.51223
#> 2.4+8  0.44619 0.26221 0.06073 0.40829 0.95072     0.15516        0.24764     0.59720
#> 3.6+8  0.50464 0.28184 0.06339 0.48516 0.97848     0.13016        0.20631     0.66353
#> 5+8    0.54764 0.29489 0.06066 0.55205 0.98990     0.12065        0.17545     0.70390
#> 6+8    0.56929 0.30157 0.05736 0.58970 0.99353     0.11880        0.15963     0.72157
#> 0.1+12 0.16861 0.10178 0.03547 0.14699 0.42186     0.55455        0.37150     0.07395
#> 0.2+12 0.19744 0.11826 0.04245 0.17231 0.49480     0.45280        0.42021     0.12699
#> 0.4+12 0.24468 0.14532 0.05306 0.21371 0.61089     0.32741        0.43966     0.23293
#> 0.8+12 0.31742 0.18591 0.06541 0.27818 0.76967     0.21384        0.38958     0.39658
#> 1.6+12 0.41223 0.23284 0.07658 0.37137 0.90767     0.14039        0.29564     0.56397
#> 2.4+12 0.47085 0.25807 0.07755 0.44007 0.95526     0.11903        0.24141     0.63956
#> 3.6+12 0.52609 0.28065 0.07099 0.51750 0.98145     0.11237        0.19308     0.69455
#> 5+12   0.56553 0.29818 0.05881 0.58437 0.99198     0.11701        0.16055     0.72244
#> 6+12   0.58456 0.30825 0.04911 0.62246 0.99526     0.12328        0.14559     0.73113
#> 
#> 
#> [[7]]
#> [[7]]$`trial-A`
#>          mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+0 0.04107 0.04924 0.00043 0.02345 0.17909     0.96468        0.03372     0.00160
#> 0.2+0 0.06287 0.06327 0.00156 0.04278 0.23383     0.91703        0.07808     0.00489
#> 0.4+0 0.10298 0.09030 0.00423 0.07765 0.33752     0.78440        0.18784     0.02776
#> 0.8+0 0.17426 0.14502 0.00872 0.13480 0.54760     0.57015        0.28477     0.14508
#> 1.6+0 0.27667 0.21783 0.01473 0.21921 0.80490     0.38519        0.28245     0.33236
#> 2.4+0 0.34253 0.25489 0.01879 0.28040 0.90423     0.30748        0.25768     0.43484
#> 3.6+0 0.40680 0.28307 0.02328 0.34997 0.95731     0.24851        0.22889     0.52260
#> 5+0   0.45561 0.29927 0.02711 0.41235 0.97881     0.21277        0.20469     0.58254
#> 6+0   0.48110 0.30597 0.02927 0.44877 0.98594     0.19524        0.19310     0.61166
#> 
#> [[7]]$`trial-B`
#>           mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+8  0.11369 0.08215 0.01366 0.09462 0.32360     0.77678        0.20059     0.02263
#> 0.2+8  0.13562 0.09562 0.01829 0.11356 0.37909     0.69106        0.26402     0.04492
#> 0.4+8  0.17336 0.12013 0.02564 0.14466 0.48312     0.55616        0.34117     0.10267
#> 0.8+8  0.23644 0.16176 0.03527 0.19611 0.65544     0.39261        0.37683     0.23056
#> 1.6+8  0.32773 0.21739 0.04580 0.27414 0.84625     0.25927        0.33264     0.40809
#> 2.4+8  0.38855 0.24900 0.05067 0.33365 0.92292     0.20827        0.28655     0.50518
#> 3.6+8  0.44901 0.27590 0.05227 0.40395 0.96624     0.17497        0.23832     0.58671
#> 5+8    0.49494 0.29417 0.05008 0.46720 0.98430     0.15997        0.20190     0.63813
#> 6+8    0.51859 0.30336 0.04690 0.50519 0.99022     0.15582        0.18457     0.65961
#> 0.1+12 0.15221 0.08991 0.03285 0.13417 0.37594     0.61827        0.33582     0.04591
#> 0.2+12 0.17321 0.10106 0.03870 0.15281 0.42447     0.53061        0.39281     0.07658
#> 0.4+12 0.20941 0.12245 0.04733 0.18385 0.51609     0.41087        0.44202     0.14711
#> 0.8+12 0.27006 0.16073 0.05769 0.23394 0.67608     0.28076        0.42922     0.29002
#> 1.6+12 0.35803 0.21441 0.06621 0.31123 0.85821     0.18857        0.34417     0.46726
#> 2.4+12 0.41660 0.24654 0.06669 0.37020 0.93059     0.15941        0.28329     0.55730
#> 3.6+12 0.47438 0.27603 0.05989 0.44150 0.97139     0.14850        0.22411     0.62739
#> 5+12   0.51736 0.29837 0.04842 0.50651 0.98789     0.15118        0.18277     0.66605
#> 6+12   0.53878 0.31060 0.04001 0.54503 0.99295     0.15636        0.16319     0.68045
#> 
#> 
#> [[8]]
#> [[8]]$`trial-A`
#>          mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+0 0.03306 0.04007 0.00032 0.01892 0.14553     0.98176        0.01781     0.00043
#> 0.2+0 0.05178 0.05267 0.00120 0.03502 0.19503     0.95110        0.04730     0.00160
#> 0.4+0 0.08759 0.07862 0.00340 0.06522 0.29536     0.84184        0.14363     0.01453
#> 0.8+0 0.15450 0.13497 0.00728 0.11586 0.51412     0.62893        0.26020     0.11087
#> 1.6+0 0.25497 0.21270 0.01266 0.19266 0.79321     0.43361        0.27358     0.29281
#> 2.4+0 0.32107 0.25277 0.01640 0.25071 0.90094     0.34750        0.25593     0.39657
#> 3.6+0 0.38635 0.28352 0.02024 0.31869 0.95758     0.28067        0.23195     0.48738
#> 5+0   0.43636 0.30143 0.02354 0.38032 0.97980     0.24004        0.20898     0.55098
#> 6+0   0.46261 0.30893 0.02567 0.41675 0.98673     0.22006        0.19818     0.58176
#> 
#> [[8]]$`trial-B`
#>           mean      sd  q.2.5%   q.50% q.97.5% P([0,0.16)) P([0.16,0.33)) P([0.33,1])
#> 0.1+8  0.09138 0.06342 0.01104 0.07747 0.25118     0.86816        0.12625     0.00559
#> 0.2+8  0.10884 0.07303 0.01509 0.09309 0.29139     0.79879        0.18753     0.01368
#> 0.4+8  0.14135 0.09474 0.02144 0.12001 0.38402     0.66708        0.28553     0.04739
#> 0.8+8  0.20064 0.14033 0.03054 0.16548 0.57193     0.48151        0.36203     0.15646
#> 1.6+8  0.29220 0.20583 0.03981 0.23645 0.81067     0.32176        0.33846     0.33978
#> 2.4+8  0.35528 0.24340 0.04414 0.29253 0.90788     0.25585        0.29750     0.44665
#> 3.6+8  0.41885 0.27509 0.04554 0.35960 0.96243     0.21052        0.25397     0.53551
#> 5+8    0.46762 0.29589 0.04289 0.42272 0.98343     0.18912        0.21588     0.59500
#> 6+8    0.49297 0.30599 0.04019 0.46165 0.98977     0.18203        0.19545     0.62252
#> 0.1+12 0.12938 0.07330 0.02905 0.11540 0.30764     0.72073        0.26244     0.01683
#> 0.2+12 0.14614 0.08079 0.03421 0.13107 0.34354     0.63959        0.32973     0.03068
#> 0.4+12 0.17738 0.09910 0.04212 0.15809 0.42293     0.50796        0.41295     0.07909
#> 0.8+12 0.23449 0.14065 0.05171 0.20333 0.59697     0.35318        0.43979     0.20703
#> 1.6+12 0.32294 0.20356 0.05913 0.27372 0.82331     0.23534        0.36822     0.39644
#> 2.4+12 0.38392 0.24123 0.05927 0.32939 0.91729     0.19522        0.30568     0.49910
#> 3.6+12 0.44512 0.27499 0.05315 0.39748 0.96792     0.17594        0.24301     0.58105
#> 5+12   0.49138 0.29939 0.04260 0.46209 0.98670     0.17329        0.19647     0.63024
#> 6+12   0.51482 0.31231 0.03513 0.50208 0.99235     0.17616        0.17270     0.65114
#> 
#> 
#> attr(,"rng")
#> attr(,"rng")[[1]]
#> [1]       10407  2133139108  -773071531  -244150766 -1207652757  1191582384  1240354545
#> 
#> attr(,"doRNG_version")
#> [1] "1.7.4"

Here, except for the first argument, data.list, we have provided precisely the same arguments as for the call to scenario_jointBLRM from the previous section. This would also work for all other (optional) arguments of scenario_jointBLRM, except for file.name. Instead of this argument, scenario_list_jointBLRM uses the optional argument file.names (notice the plural), which has the same function as file.name for scenario_jointBLRM, but needs to contain a vector with a file name for each scenario instead. As before, the argument is ignored unless you want to save the output and have supplied a path.

Note further that the historical data provided to scenario_list_jointBLRM is included in the posterior evaluations for every scenario, i.e., the historical data is interpreted in the same fashion as for scenario_jointBLRM, and does not vary across the scenarios in the list.

To obtain a prior configuration, it is now recommended to create a sufficiently large number of scenarios, and repeatedly evaluate the scenarios to gradually alter the prior distribution and obtain an appropriate setup and behavior in the considered scenarios. However, as mentioned before, one will probably not be able to consider every potential scenario in advance, so that this is mostly a heuristic check and is not guaranteed to yield an optimal prior. Due to this, further evaluation of the prior should be performed to confirm that it shows appropriate operating characteristics in the long-run. This will be the subject of the following section.

Simulating dose-finding trials with sim_jointBLRM

Simulations of trials usually aim to estimate the operating characteristics (OC) of a dose-finding trial design, which includes e.g. the ratio of MTDs declared on each dose (or on doses with DLT rate in a specific dosing interval), the number of patients per dose and the number of DLTs in the trial, as well as further metrics for the simulation results.

To estimate the operating characteristics of the BLRM, one usually uses simulated trials. That is, one assumes a fixed set of available dose levels and a fixed dose-toxicity scenario – i.e. a specification of the DLT rate for each available dose level – and simulates a number of trials in this setting. This allows to e.g. estimate the average number of MTDs in the correct interval or the number of patients treated at overly toxic doses for this specific dose-toxicity scenario.

As it is of course not possible to test all possible dose-toxicity scenarios, one will typically confine oneself to a selected number of scenarios that illustrate different possible cases. These should usually range from scenarios that follow the prior expectations, over more extreme scenarios that assume the involved drugs to be considerably more (or less) toxic than expected by the prior, up to scenarios that deliberately assume the trials to result in heterogeneous data or that the true dose-toxicity relationship does not follow the logistic model of the BLRM (i.e. one assumes the BLRM to be misspecified).

As an example how such simulations can be performed via sim_jointBLRM, we will again consider the setting of the previous section. For this, recall that a monotherapy and combination therapy trial shall run (partially) in parallel, where we wanted to consider the dose levels given in the variable doses.of.interest and use the data from a historical trial as given in the historical.data argument.

The function sim_jointBLRM supports simulation of (parallel) monotherapy or combination therapy trials. Internally, it is differentiated between three types, namely monotherapy for compound 1 ("mono1"), monotherapy for compound 2 ("mono2"), and combination therapy with compounds 1 and 2 ("combi"). For each of these types, the function can actively simulate 2 trials (i.e., six parallel trials in total), and the order in which cohorts are enrolled in each of the up to six trials can be specified freely. The simulated trials can be activated independently of each other, i.e. one can choose how many of the parallel trials are simulated.

Additionally, historical data from arbitrarily many trials that are already concluded can be given, and furthermore, data that was observed in the actively simulated trials before the start of the simulation can be included as well (which allows to simulate how one or more trials might continue after already having observed a specific data scenario).

Naming conventions for sim_jointBLRM

The function features a large number of optional parameters to allow relatively flexible customization of the simulated trials, e.g. regarding the number of patients per cohort, criteria for MTD selection, escalation rules, and further topics. Refer to the documentation for more detail and the parameters that are not discussed in this vignette.

To allow some settings to deviate across the simulated trials, many of the arguments of sim_jointBLRM exist in six variations, one for each simulated trial. To differentiate between these, the arguments feature trial-specific suffixes as given in the following table.

Trial	Suffix of function arguments
1st monotherapy trial for compound 1	mono1.a
1st monotherapy trial for compound 2	mono2.a
1st combination therapy trial	combi.a
2nd monotherapy trial for compound 1	mono1.b
2nd monotherapy trial for compound 2	mono2.b
2nd combination therapy trial	combi.b

Here, the first and second trial for a specific trial type mean simply that these are independently escalating trials of the same type, but does not imply a specific order or some other dependency across the first and second trial (except that they are jointly modeled in the BLRM). It is for instance possible to just simulate the mono2.b trial and deactivate all other trials.

The take away message from these naming conventions is that one needs to use the parameter with the corresponding suffix when an specific option shall only affect one specific trial but not the others. Arguments that do not have a suffix will in general always affect all simulated trials.

Apart from the argument names, the suffixes for the six potentially simulated trials are also used to refer to the corresponding trial when the order in which the trials enroll cohorts is specified. Furthermore, they are also used to encode the trials when historical data that was previously recorded in an actively simulated trial shall be included. Refer to the documentation for more detail.

Configuring the trial simulations

First and foremost, one needs to decide which of the possible six trials need to be simulated and activate the corresponding trials. For the example in this vignette, an monotherapy trial for compound 1 and a combination therapy trial shall be included. We will assume that we have chosen to utilize the mono1.a and combi.a trials to represent these trials (although it would be equivalent to use the mono1.b and combi.b trials or even a combination of mono1.b and combi.a). To activate the trials, we can supply the arguments

active.mono1.a = TRUE
active.combi.a = TRUE

Now, we specify the corresponding available dose levels. For this, we will use the same doses as specified previously:

doses.mono1.a = c(0.1, 0.2, 0.4, 0.8, 1.6, 2.4, 3.6, 5, 6)

doses.combi.a = rbind(
  rep(doses.mono1.a, times=2),
  rep(c(8, 12),      each = length(doses.mono1.a)))

Note that doses.mono1.a is a vector, while doses.combi.a needs to be a matrix with two rows, so that each column specifies a dose combination to be considered in the combination therapy trial. The code above generated every possible combination of the doses from the monotherapy trial for compound 1 with the doses 8 and 12 for compound 2.

As for the function scenario_jointBLRM, one again needs to specify reference doses and a prior distribution for the BLRM. For this, the same argument names and formats as for scenario_jointBLRM are used, i.e. the arguments dose.ref1, dose.ref2, prior.mu, and prior.tau can be used in the form that was specified in the previous section. The same holds for the historical data, for which we will assume that the same observations as before are used, namely

historical.data
#> $dose1
#> [1] 0 0 0 0 0
#> 
#> $dose2
#> [1]  2  4  8 12 16
#> 
#> $n.pat
#> [1]  3  3  3  9 12
#> 
#> $n.dlt
#> [1] 0 0 0 1 2
#> 
#> $trial
#> [1] "H1" "H1" "H1" "H1" "H1"

Additionally, we need to provide starting dose levels for each activated trials. Note that these must be elements of the set of available dose levels, otherwise the function will report an error. We will assume that the monotherapy trial will start with the lowest available dose, 0.1, which is specified via

start.dose.mono1.a = 0.1

We will later assume additionally that the monotherapy trial enrolls at least 3 or 4 cohorts before the first combination therapy cohort is processed, and due to this, we assume the combination trial to use a slightly larger starting dose. For instance, suppose that the combination therapy shall begin with the dose combination of 0.2 of compound 1 and 8 of compound 2. This is expressed by using

start.dose.combi.a1 = 0.2
start.dose.combi.a2 = 8

Note that two arguments need to be specified for this, with suffix .combi.a1 for the first compound and .combi.a2 for the second compound. Both of these arguments belong to the combi.a trial, while the endings .a1 and .a2 are used to differentiate between the setting for the first and second compound of the combi.a trial. They are also used for other arguments that may need different settings for the two combination therapy partners in the same combination therapy trial.

Optional general specification

As a next step, the general course of the trial can be defined, consisting of the number of patients per cohort, the maximum number of patients in the trial, and the order in which cohorts are enrolled. All of these arguments are optional, and relatively sensible defaults will be used when they are not specified.

First, to set the number of patients per cohort, one can use e.g.

cohort.size = 3

Note that cohort.size is the global variant of this argument, i.e. it affects all simulated trials. If it is not provided explicitly, the function will use the default value of 3. If a specific trial shall deviate from this value, one can use the trial-specific parameter with the corresponding trial suffix, e.g.

cohort.size.mono1.b = 4

Note that this would only affect the mono1.b trial, which we do not plan to simulate in the current example. For the mono1.a and combi.a trial, which we do want to simulate, the global cohort size of 3 is still in effect. The same would apply if cohort.size is not given to the function, as the default value would have been used in this case.

One can also provide a vector of multiple cohort sizes, in which case the function will randomly select one of the given cohort sizes for each cohort. The cohort sizes will then be drawn uniformly at random from the possible numbers specified in ‘cohort.size’ if no further options are given. If it is desired to draw each cohort size with a specific probability, one can use the optional argument cohort.prob to provide the probability for each cohort size, e.g. by setting

cohort.size.mono1.b = c(2,    3,    4)
cohort.prob.mono1.b = c(0.05, 0.85, 0.1)

In this example, the mono1.b trial would select the size of each cohort randomly according to the corresponding probabilities, i.e. a cohort size of 2 is drawn with a probability of 0.05, a size of 3 with probability 0.85, and a cohort size of 4 will be chosen with a probability of 0.1. As before, there is a global and trial-specific version of the argument cohort.prob.

As a next step, we want to set the maximum number of patients for each trial. We will assume the maximum number of patients to be 36 for the combination therapy trial and 45 for the monotherapy trial. This can be set via the trial-specific arguments

max.n.mono1.a = 45
max.n.combi.a = 36

Note that there is also a global argument max.n, which will not be used in this example.

Now, the order in which cohorts are enrolled is specified. For this, the function uses the argument cohort.queue, which provides, as the name says, a queue of cohorts that is processed during the simulation. This can be done by supplying a simple pattern which is automatically repeated (note however that the function will drop a warning in this case) or by supplying a complex pattern that already contains every cohort that may potentially be arriving throughout the trial. For instance, to simply simulate cohorts for mono1.a and combi.a alternately, one can use

cohort.queue = c("mono1.a", "combi.a")

This order would then be repeated until both trials concluded due to being stopped early, having found an MTD, or reaching the maximum patient number.

The cohort queue is mostly used to enforce a specific order of the cohorts in a trial. For this, consider again the example from the previous section, where a monotherapy and combination trial shall be simulated in parallel. Assume for instance that one wants to start the combination therapy trial after the first four monotherapy cohorts were processed, and, afterwards, the trials shall enroll cohorts alternately. This is expressed by setting the queue to

cohort.queue = c("mono1.a", "mono1.a", "mono1.a", rep(c("mono1.a", "combi.a"),
                                                      times=12))
head(cohort.queue, 9)
#> [1] "mono1.a" "mono1.a" "mono1.a" "mono1.a" "combi.a" "mono1.a" "combi.a" "mono1.a" "combi.a"

Note that c("mono1.a", "combi.a") is repeated 12 times, which translates to 12 "combi.a" and 15 "mono1.a" cohorts in the queue. As the cohort size was previously set to 3 patients, this results in a total of 36 patients for combi.a in the queue and 45 patients for mono1.a, i.e. precisely the maximum sample size that was specified. This ensures that the function will not need to repeat the queue automatically. Note that it would not be a problem to provide a cohort queue containing more patients than required, as the function will simply ignore cohorts for each simulated trial once it has concluded. Therefore, it is also possible to use e.g.

cohort.queue = c("mono1.a", "mono1.a", "mono1.a", rep(c("mono1.a", "combi.a"),
                                                      times=100))

Here, we supplied much more cohorts than needed (100 for combination therapy), which is still equivalent to the previous queue. Only supplying lower numbers of cohorts will cause the function to operate differently, as it will repeat the cohort queue until all trials concluded.

Note that the trials in the cohort queue can also be indicated with numbers (which usually leads to shorter code than the full trial names), as stated in the following table.

Trial	Suffix of function arguments	Number
1st monotherapy trial for compound 1	mono1.a	1
1st monotherapy trial for compound 2	mono2.a	2
1st combination therapy trial	combi.a	3
2nd monotherapy trial for compound 1	mono1.b	4
2nd monotherapy trial for compound 2	mono2.b	5
2nd combination therapy trial	combi.b	6

Hence, the previous cohort queue could be equivalently written as

cohort.queue = c(1, 1, 1, rep(c(1, 3), times=100))

Escalation decisions in simulted trials

As a next step, we specify rules for dose escalation decisions. As mentioned before, the function will by default apply EWOC-based escalation, which means that only doses can be chosen for which the posterior probability of overdosing is below 0.25. This boundary could also be altered, by using the argument

ewoc.threshold = 0.25

As EWOC only states an upper boundary, the function will afterwards maximize the probability of having a DLT rate within the target interval among the doses that satisfy EWOC. If this still leads to multiple possible doses, the function will subsequently maximize the dose of the first compound among the doses with the same probability of target dosing. To maximize the second compound instead, one can set the argument esc.comp.max, which may have the values 1 or 2 and indicates which component the function will maximize in case of draws. Note that one can also deviate from maximizing the target probability and maximize directly the dose among the levels that satisfy EWOC, but this is not covered in this vignette. Refer to the documentation of the argument esc.rule for information on this.

Neuenschwander et al. (2014) recommend to impose a maximum increment of the dose additionally to EWOC, in order to avoid overly large dosing steps during dose escalations. This can be realized by using the esc.step family of arguments, which is available as a global variant and six trial-specific parameters. The escalation step is interpreted as the maximum factor of dose escalation. For instance, when an escalation step is set to the value 2, the dose can at most be doubled in each escalation decision. If no escalation step is given, the function will set it to the maximum factor between subsequent dose levels as an additional constrain on the escalation.

However, there might be situations in which one may not want a fixed maximum factor between escalations, e.g. if a factor cannot express the increments between planned dose levels. Consider for instance a trial with planned doses of 10, 20, 30, and 40 mg. In order to allow escalating from 10 to 20, the escalation step would need to be set to 2, but this would also allow escalating from 20 to 40 without enrolling patients at 30. To prevent this, one can set

esc.constrain = TRUE

This argument constrains escalations to the given set of dose levels, i.e. only the next larger prespecified dose can be used. If activated, esc.constrain causes the function to ignore any given escalation step and always restrict escalation decisions to the next larger dose (but does not pose a boundary when deescalating the dose). As before, esc.constrain is the global variant, while additional arguments like esc.constrain.mono1.b only affect the corresponding trial.

MTD selection

It now remains to specify the rules for MTD selection in the trial.

There are two different arguments that control how the function selects the MTD of a simulated trial, namely mtd.decision and mtd.enforce. Both are available as global arguments without suffix and as trial-specific argument with the corresponding suffix. The argument mtd.decision is a named list with five entries of the form

mtd.decision = list(
  min.dlt     = 1,
  pat.at.mtd  = 6,
  min.pat     = 12,
  target.prob = 0.5,
  rule        = 2
)

The list stated above is also the default argument. The first four list entries correspond to the demanded boundaries of four different conditions that are used to determine an MTD. The last entry, mtd.decision$rule does not pose a condition itself, but dictates which of the other conditions are mandatory instead.

During the simulation, the MTD can only be determined as the dose that was used for the last cohort, which is always the current candidate for the MTD. For MTD selection, the function will then first demand that the current dose level is also recommended for the next cohort again (so-called stabilization criterion). If this is the case, it will check whether the current dose also satisfies the conditions determined by mtd.decision, and, if these are satisfied, declare the current dose to be the MTD of this trial. The precise conditions and the corresponding entries in mtd.decision are listed in the following table.

No.	List entry	Condition
1	min.dlt	At least min.dlt patients with DLTs were observed in the trial.
2	pat.at.mtd	At least pat.at.mtd patients were treated with the current dose.
3	min.pat	At least min.pat patients were treated in the current trial.
4	target.prob	The probability that the current dose has DLT rate in the target interval is at least target.prob.

In terms of the effect of the entry rule, the following to possibilities are supported

• If rule is 1: Conditions 1 and 2 are necessary, and at least one of conditions 3 and 4 must be satisfied as well.

• If rule is 2: Conditions 1 and 3 are necessary, and at least one of conditions 2 and 4 must be satisfied as well.

Other decision rule specifications may be supported in the future.

The second argument that affects MTD selection, mtd.enforce, is a logical value that controls how the function behaves when a trial reaches the specified maximum sample size. By default, mtd.enforce is FALSE, which causes trials that reach the maximum sample size to be considered as not having found an MTD, which will also be noted in the output. If the parameter is instead TRUE, the current dose will be considered the MTD when the maximum sample size is reached before the conditions for MTD selections are satisfied. This can e.g. be used if one wants to approximate the average dosing recommendations after a specific number of cohorts based on simulations. For instance, when max.n = 15, mtd.enforce = TRUE, one can set mtd.decision to values that cannot be reached within 15 patients (e.g., mtd.decision$rule = 2 and mtd.decision$min.pat = 16), so that the function will simply report the dosing recommendation after 15 patients as the MTD and not apply the MTD decision rule. This option can also be set for individual trials (via the parameters with the corresponding suffix).

Dose-toxicity scenarios and trial simulations

It remains to specify a dose-toxicity scenario before the simulation can be started. That is, a DLT rate for each dose level is assumed, which is then used by the function to simulate the number of patients experiencing DLT in each cohort.

The arguments for specifying the DLT rate in one of the simulated trials are named according to the pattern tox.[...], where [...] can be any of the trial-specific suffixes. Note that there is no global variant of this argument. For the situation discussed in the previous chapters, the required arguments are therefore tox.mono1.a and tox.combi.a.

First, recall the specification of the dose levels for the monotherapy trial:

doses.mono1.a
#> [1] 0.1 0.2 0.4 0.8 1.6 2.4 3.6 5.0 6.0

The DLT rates (or toxicities) must therefore be specified for 9 dose levels. This is done by supplying a vector of this length, so that the entry tox.mono1.a[i] specifies the DLT rate of the dose given in doses.mono1.a[i]. In our case, this could e.g. be

#Compound 1:     0.1   0.2   0.4   0.8   1.6   2.4   3.6   5     6
tox.mono1.a = c(0.01, 0.02, 0.03, 0.05, 0.09, 0.12, 0.19, 0.29, 0.43)

Similarly, for the combination therapy trial, the dose levels were given as

doses.combi.a
#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] [,18]
#> [1,]  0.1  0.2  0.4  0.8  1.6  2.4  3.6    5    6   0.1   0.2   0.4   0.8   1.6   2.4   3.6     5     6
#> [2,]  8.0  8.0  8.0  8.0  8.0  8.0  8.0    8    8  12.0  12.0  12.0  12.0  12.0  12.0  12.0    12    12

Here, each column specifies a dose, so that the argument tox.combi.a needs one entry for each column, i.e. 18 entries in our example. Similarly to before, entry i of the argument provides the DLT rate of the dose given in column i of doses.combi.a. Hence, a dose-toxicity scenario for this case could be

#Compound 1:     0.1   0.2   0.4   0.8   1.6   2.4   3.6   5     6        0.1   0.2   0.4   0.8   1.6   2.4   3.6   5     6
#compound 2:     8     8     8     8     8     8     8     8     8        12    12    12    12    12    12    12    12    12
tox.combi.a = c(0.02, 0.03, 0.04, 0.08, 0.14, 0.21, 0.32, 0.39, 0.47,    0.04, 0.06, 0.09, 0.12, 0.17, 0.29, 0.45, 0.52, 0.61)

Note that one will usually consider multiple different dose toxicity scenarios to assess the performance of the prior in different settings and situations. In the following, we will only consider the scenario specified above for simplicity.

This completes the setup and specification of the trials that are to be simulated. As a last step, it remains to specify the number of simulated studies via the parameter n.studies. As an example, 1 study will be used in the following. Note however that this is of course by far not sufficient for a proper evaluation of the prior, where one should simulate something around the order of e.g. 1000 to 10000 studies. However, be aware that depending on the specifications, each study will require up to multiple minutes of run time for the repeated calls to Stan, so that 1000 or more trials may take multiple hours or even nearly a day to simulate. It is therefore recommended to run the simulation in parallel.

If a cluster is available, a parallel backend consisting of multiple nodes with multiple cores can be registered, so that the function can leverage the capabilities of a cluster with a nested foreach loop. This is however purely optional. Further, when running simulations in parallel with a moderate number of cores, it is recommended to consider the argument working.path in the documentation, as this allows to save a reload MCMC results across nodes and cores.

At last, one can also optionally specify the arguments path and file.name, which will cause the function to automatically write the summarized simulation results to a .xlsx file of the specified name under the specified path. Otherwise, the simulation results are only returned to R.

Putting all of the previous explanations together, the call to sim_jointBLRM would therefore be:

sim_result <- sim_jointBLRM(
  active.mono1.a = TRUE,
  active.combi.a = TRUE,

  doses.mono1.a = doses.mono1.a,
  doses.combi.a = doses.combi.a,
  dose.ref1 = dose.ref1,
  dose.ref2 = dose.ref2,
  start.dose.mono1.a = start.dose.mono1.a,
  start.dose.combi.a1 = start.dose.combi.a1,
  start.dose.combi.a2 = start.dose.combi.a2,

  tox.mono1.a = tox.mono1.a,
  tox.combi.a = tox.combi.a,

  historical.data = historical.data,
  prior.mu = prior.mu,
  prior.tau = prior.tau,

  max.n.mono1.a = max.n.mono1.a,
  max.n.combi.a = max.n.combi.a,
  cohort.size = cohort.size,
  cohort.queue = cohort.queue,
  ewoc.threshold = ewoc.threshold,
  esc.constrain = esc.constrain,
  mtd.decision = mtd.decision,

  n.studies = 1
)

print(sim_result)
#> $`results combi.a`
#>                              underdose target dose overdose max n reached before MTD all doses too toxic
#> Number of trials                     0           1        0                        0                   0
#> Percentage                           0         100        0                        0                   0
#> Percentage not all too toxic         0         100        0                        0                  NA
#> 
#> $`summary combi.a`
#>                      Median       Mean       Min.       Max.       2.5%      97.5%
#> #Pat underdose    9.0000000  9.0000000  9.0000000  9.0000000  9.0000000  9.0000000
#> #Pat target dose  6.0000000  6.0000000  6.0000000  6.0000000  6.0000000  6.0000000
#> #Pat overdose     0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> #Pat (all)       15.0000000 15.0000000 15.0000000 15.0000000 15.0000000 15.0000000
#> #DLT underdose    1.0000000  1.0000000  1.0000000  1.0000000  1.0000000  1.0000000
#> #DLT target dose  1.0000000  1.0000000  1.0000000  1.0000000  1.0000000  1.0000000
#> #DLT overdose     0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> #DLT (all)        2.0000000  2.0000000  2.0000000  2.0000000  2.0000000  2.0000000
#> % overdose        0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> % DLT             0.1333333  0.1333333  0.1333333  0.1333333  0.1333333  0.1333333
#> 
#> $`MTDs combi.a`
#>                  0.1+8       0.2+8       0.4+8       0.8+8       1.6+8       2.4+8         3.6+8         5+8       
#> Dose             "0.1+8"     "0.2+8"     "0.4+8"     "0.8+8"     "1.6+8"     "2.4+8"       "3.6+8"       "5+8"     
#> True P(DLT)      "0.02"      "0.03"      "0.04"      "0.08"      "0.14"      "0.21"        "0.32"        "0.39"    
#> True category    "underdose" "underdose" "underdose" "underdose" "underdose" "target dose" "target dose" "overdose"
#> MTD declared (n) "0"         "0"         "0"         "0"         "0"         "0"           "0"           "0"       
#>                  6+8        0.1+12      0.2+12      0.4+12      0.8+12      1.6+12        2.4+12        3.6+12    
#> Dose             "6+8"      "0.1+12"    "0.2+12"    "0.4+12"    "0.8+12"    "1.6+12"      "2.4+12"      "3.6+12"  
#> True P(DLT)      "0.47"     "0.04"      "0.06"      "0.09"      "0.12"      "0.17"        "0.29"        "0.45"    
#> True category    "overdose" "underdose" "underdose" "underdose" "underdose" "target dose" "target dose" "overdose"
#> MTD declared (n) "0"        "0"         "0"         "0"         "0"         "0"           "1"           "0"       
#>                  5+12       6+12      
#> Dose             "5+12"     "6+12"    
#> True P(DLT)      "0.52"     "0.61"    
#> True category    "overdose" "overdose"
#> MTD declared (n) "0"        "0"       
#> 
#> $`#pat. combi.a`
#>             0.1+8   0.2+8   0.4+8   0.8+8   1.6+8   2.4+8   3.6+8   5+8   6+8   0.1+12   0.2+12   0.4+12   0.8+12  
#> Dose        "0.1+8" "0.2+8" "0.4+8" "0.8+8" "1.6+8" "2.4+8" "3.6+8" "5+8" "6+8" "0.1+12" "0.2+12" "0.4+12" "0.8+12"
#> mean #pat   "0"     "3"     "0"     "0"     "0"     "0"     "0"     "0"   "0"   "0"      "0"      "3"      "3"     
#> median #pat "0"     "3"     "0"     "0"     "0"     "0"     "0"     "0"   "0"   "0"      "0"      "3"      "3"     
#> min #pat    "0"     "3"     "0"     "0"     "0"     "0"     "0"     "0"   "0"   "0"      "0"      "3"      "3"     
#> max #pat    "0"     "3"     "0"     "0"     "0"     "0"     "0"     "0"   "0"   "0"      "0"      "3"      "3"     
#>             1.6+12   2.4+12   3.6+12   5+12   6+12  
#> Dose        "1.6+12" "2.4+12" "3.6+12" "5+12" "6+12"
#> mean #pat   "3"      "3"      "0"      "0"    "0"   
#> median #pat "3"      "3"      "0"      "0"    "0"   
#> min #pat    "3"      "3"      "0"      "0"    "0"   
#> max #pat    "3"      "3"      "0"      "0"    "0"   
#> 
#> $`#DLT combi.a`
#>             0.1+8   0.2+8   0.4+8   0.8+8   1.6+8   2.4+8   3.6+8   5+8   6+8   0.1+12   0.2+12   0.4+12   0.8+12  
#> Dose        "0.1+8" "0.2+8" "0.4+8" "0.8+8" "1.6+8" "2.4+8" "3.6+8" "5+8" "6+8" "0.1+12" "0.2+12" "0.4+12" "0.8+12"
#> mean #DLT   "0"     "0"     "0"     "0"     "0"     "0"     "0"     "0"   "0"   "0"      "0"      "0"      "1"     
#> median #DLT "0"     "0"     "0"     "0"     "0"     "0"     "0"     "0"   "0"   "0"      "0"      "0"      "1"     
#> min #DLT    "0"     "0"     "0"     "0"     "0"     "0"     "0"     "0"   "0"   "0"      "0"      "0"      "1"     
#> max #DLT    "0"     "0"     "0"     "0"     "0"     "0"     "0"     "0"   "0"   "0"      "0"      "0"      "1"     
#>             1.6+12   2.4+12   3.6+12   5+12   6+12  
#> Dose        "1.6+12" "2.4+12" "3.6+12" "5+12" "6+12"
#> mean #DLT   "0"      "1"      "0"      "0"    "0"   
#> median #DLT "0"      "1"      "0"      "0"    "0"   
#> min #DLT    "0"      "1"      "0"      "0"    "0"   
#> max #DLT    "0"      "1"      "0"      "0"    "0"   
#> 
#> $`results mono1.a`
#>                              underdose target dose overdose max n reached before MTD all doses too toxic
#> Number of trials                     0           1        0                        0                   0
#> Percentage                           0         100        0                        0                   0
#> Percentage not all too toxic         0         100        0                        0                  NA
#> 
#> $`summary mono1.a`
#>                      Median       Mean       Min.       Max.       2.5%      97.5%
#> #Pat underdose   21.0000000 21.0000000 21.0000000 21.0000000 21.0000000 21.0000000
#> #Pat target dose  6.0000000  6.0000000  6.0000000  6.0000000  6.0000000  6.0000000
#> #Pat overdose     0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> #Pat (all)       27.0000000 27.0000000 27.0000000 27.0000000 27.0000000 27.0000000
#> #DLT underdose    1.0000000  1.0000000  1.0000000  1.0000000  1.0000000  1.0000000
#> #DLT target dose  2.0000000  2.0000000  2.0000000  2.0000000  2.0000000  2.0000000
#> #DLT overdose     0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> #DLT (all)        3.0000000  3.0000000  3.0000000  3.0000000  3.0000000  3.0000000
#> % overdose        0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> % DLT             0.1111111  0.1111111  0.1111111  0.1111111  0.1111111  0.1111111
#> 
#> $`MTDs mono1.a`
#>                  0.1         0.2         0.4         0.8         1.6         2.4         3.6           5            
#> Dose             "0.1"       "0.2"       "0.4"       "0.8"       "1.6"       "2.4"       "3.6"         "5"          
#> True P(DLT)      "0.01"      "0.02"      "0.03"      "0.05"      "0.09"      "0.12"      "0.19"        "0.29"       
#> True category    "underdose" "underdose" "underdose" "underdose" "underdose" "underdose" "target dose" "target dose"
#> MTD declared (n) "0"         "0"         "0"         "0"         "0"         "0"         "1"           "0"          
#>                  6         
#> Dose             "6"       
#> True P(DLT)      "0.43"    
#> True category    "overdose"
#> MTD declared (n) "0"       
#> 
#> $`#pat. mono1.a`
#>             0.1   0.2   0.4   0.8   1.6   2.4   3.6   5   6  
#> Dose        "0.1" "0.2" "0.4" "0.8" "1.6" "2.4" "3.6" "5" "6"
#> mean #pat   "3"   "3"   "3"   "6"   "3"   "3"   "6"   "0" "0"
#> median #pat "3"   "3"   "3"   "6"   "3"   "3"   "6"   "0" "0"
#> min #pat    "3"   "3"   "3"   "6"   "3"   "3"   "6"   "0" "0"
#> max #pat    "3"   "3"   "3"   "6"   "3"   "3"   "6"   "0" "0"
#> 
#> $`#DLT mono1.a`
#>             0.1   0.2   0.4   0.8   1.6   2.4   3.6   5   6  
#> Dose        "0.1" "0.2" "0.4" "0.8" "1.6" "2.4" "3.6" "5" "6"
#> mean #DLT   "0"   "0"   "0"   "1"   "0"   "0"   "2"   "0" "0"
#> median #DLT "0"   "0"   "0"   "1"   "0"   "0"   "2"   "0" "0"
#> min #DLT    "0"   "0"   "0"   "1"   "0"   "0"   "2"   "0" "0"
#> max #DLT    "0"   "0"   "0"   "1"   "0"   "0"   "2"   "0" "0"
#> 
#> $`historical data`
#>        Obs1 Obs2 Obs3 Obs4 Obs5
#> Dose 1    0    0    0    0    0
#> Dose 2    2    4    8   12   16
#> N Pat.    3    3    3    9   12
#> N DLT     0    0    0    1    2
#> Trial     7    7    7    7    7
#> 
#> $prior
#>               mean        SD
#> mu_a1   -0.7081851 3.0000000
#> mu_b1    0.0000000 1.0000000
#> mu_a2   -0.7081851 3.0000000
#> mu_b2    0.0000000 1.0000000
#> mu_eta   0.0000000 1.1210000
#> tau_a1  -1.3862944 0.3536465
#> tau_b1  -2.0794415 0.3536465
#> tau_a2  -1.3862944 0.3536465
#> tau_b2  -2.0794415 0.3536465
#> tau_eta -2.0794415 0.3536465
#> 
#> $specifications
#>                                  Value       -     
#> seed                             "558535265" "-"   
#> dosing.intervals                 "0.16"      "0.33"
#> esc.rule                         "ewoc"      "-"   
#> esc.comp.max                     "1"         "-"   
#> dose.ref1                        "6"         "-"   
#> dose.ref2                        "12"        "-"   
#> saturating                       "FALSE"     "-"   
#> ewoc.threshold                   "0.25"      "-"   
#> start.dose.mono1.a               "0.1"       "-"   
#> esc.step.mono1.a                 "2"         "-"   
#> esc.constrain.mono1.a            "TRUE"      "-"   
#> max.n.mono1.a                    "45"        "-"   
#> cohort.size.mono1.a              "3"         "-"   
#> cohort.prob.mono1.a              "1"         "-"   
#> mtd.decision.mono1.a$target.prob "0.5"       "-"   
#> mtd.decision.mono1.a$pat.at.mtd  "6"         "-"   
#> mtd.decision.mono1.a$min.pat     "12"        "-"   
#> mtd.decision.mono1.a$min.dlt     "1"         "-"   
#> mtd.decision.mono1.a$rule        "2"         "-"   
#> mtd.enforce.mono1.a              "FALSE"     "-"   
#> backfill.mono1.a                 "FALSE"     "-"   
#> backfill.size.mono1.a            "3"         "-"   
#> backfill.prob.mono1.a            "1"         "-"   
#> backfill.start.mono1.a           "0.1"       "-"   
#> start.dose.combi.a1              "0.2"       "-"   
#> start.dose.combi.a2              "8"         "-"   
#> esc.step.combi.a1                "2"         "-"   
#> esc.step.combi.a2                "1.5"       "-"   
#> esc.constrain.combi.a1           "TRUE"      "-"   
#> esc.constrain.combi.a2           "TRUE"      "-"   
#> max.n.combi.a                    "36"        "-"   
#> cohort.size.combi.a              "3"         "-"   
#> cohort.prob.combi.a              "1"         "-"   
#> mtd.decision.combi.a$target.prob "0.5"       "-"   
#> mtd.decision.combi.a$pat.at.mtd  "6"         "-"   
#> mtd.decision.combi.a$min.pat     "12"        "-"   
#> mtd.decision.combi.a$min.dlt     "1"         "-"   
#> mtd.decision.combi.a$rule        "2"         "-"   
#> mtd.enforce.combi.a              "FALSE"     "-"   
#> backfill.combi.a                 "FALSE"     "-"   
#> backfill.size.combi.a            "3"         "-"   
#> backfill.prob.combi.a            "1"         "-"   
#> backfill.start.combi.a1          "0.1"       "-"   
#> backfill.start.combi.a2          "8"         "-"   
#> 
#> $`Stan options`
#>                 Value
#> chains            4.0
#> iter          13500.0
#> warmup         1000.0
#> adapt_delta       0.8
#> max_treedepth    15.0

This completes the setup of the simulation function for prior evaluations. As mentioned before, it is recommended to evaluate multiple different scenarios for at least multiple hundred studies when assessing the performance of an actual design.

References

Babb, James, André Rogatko, and Shelemyahu Zacks. 1998. “Cancer Phase I Clinical Trials: Efficient Dose Escalation with Overdose Control.” Statistics in Medicine 17 (10): 1103–20. https://doi.org/10.1002/(SICI)1097-0258(19980530)17:10<1103::AID-SIM793>3.0.CO;2-9.

Neuenschwander, Beat, Michael Branson, and Thomas Gsponer. 2008. “Critical Aspects of the Bayesian Approach to Phase I Cancer Trials.” Statistics in Medicine 27 (13): 2420–39. https://doi.org/10.1002/sim.3230.

Neuenschwander, Beat, Alessandro Matano, Zhongwen Tang, Satrajit Roychoudhury, Simon Wandel, and Stuart Bailey. 2014. “A Bayesian Industry Approach to Phase I Combination Trials in Oncology.” In Statistical Methods in Drug Combination Studies, 95–135. Chapman; Hall/CRC. https://doi.org/10.1201/b17965.

Neuenschwander, Beat, Satrajit Roychoudhury, and Heinz Schmidli. 2016. “On the Use of Co-Data in Clinical Trials.” Statistics in Biopharmaceutical Research 8 (3): 345–54. https://doi.org/10.1080/19466315.2016.1174149.

Neuenschwander, Beat, Sebastian Weber, Heinz Schmidli, and Anthony O’Hagan. 2020. “Predictively Consistent Prior Effective Sample Sizes.” Biometrics 76 (2): 578–87. https://doi.org/10.1111/biom.13252.

Session info

sessionInfo()
#> R version 4.1.2 (2021-11-01)
#> Platform: x86_64-w64-mingw32/x64 (64-bit)
#> Running under: Windows 10 x64 (build 19044)
#> 
#> Matrix products: default
#> 
#> locale:
#> [1] LC_COLLATE=German_Germany.1252  LC_CTYPE=German_Germany.1252    LC_MONETARY=German_Germany.1252
#> [4] LC_NUMERIC=C                    LC_TIME=German_Germany.1252    
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] future.batchtools_0.12.0 parallelly_1.35.0        doRNG_1.8.2              rngtools_1.5.2          
#> [5] doFuture_1.0.0           future_1.32.0            foreach_1.5.2            decider_0.0.0.9011      
#> 
#> loaded via a namespace (and not attached):
#>  [1] httr_1.4.2           RcppParallel_5.1.5   StanHeaders_2.21.0-7 askpass_1.1          highr_0.9           
#>  [6] stats4_4.1.2         base64url_1.4        yaml_2.2.2           progress_1.2.2       globals_0.16.1      
#> [11] pillar_1.7.0         backports_1.4.1      glue_1.6.1           digest_0.6.29        checkmate_2.1.0     
#> [16] colorspace_2.0-3     htmltools_0.5.2      pkgconfig_2.0.3      rstan_2.21.5         listenv_0.8.0       
#> [21] purrr_0.3.4          scales_1.2.1         processx_3.8.1       brew_1.0-6           openxlsx_4.2.5.2    
#> [26] tibble_3.1.6         openssl_1.4.6        generics_0.1.1       farver_2.1.0         ggplot2_3.3.6       
#> [31] ellipsis_0.3.2       cachem_1.0.6         withr_2.5.0          cli_3.4.1            magrittr_2.0.2      
#> [36] crayon_1.5.1         memoise_2.0.1        evaluate_0.14        ps_1.6.0             fs_1.5.2            
#> [41] fansi_1.0.2          doParallel_1.0.17    pkgbuild_1.3.1       tools_4.1.2          loo_2.5.1           
#> [46] data.table_1.14.2    prettyunits_1.1.1    hms_1.1.1            lifecycle_1.0.3      matrixStats_0.62.0  
#> [51] stringr_1.4.0        munsell_0.5.0        zip_2.2.0            callr_3.7.3          pkgdown_2.0.7       
#> [56] compiler_4.1.2       rlang_1.0.6          grid_4.1.2           iterators_1.0.14     rstudioapi_0.13     
#> [61] rappdirs_0.3.3       labeling_0.4.2       rmarkdown_2.11       gtable_0.3.0         codetools_0.2-18    
#> [66] flock_0.7            inline_0.3.19        R6_2.5.1             gridExtra_2.3        knitr_1.37          
#> [71] dplyr_1.0.7          fastmap_1.1.0        future.apply_1.9.1   utf8_1.2.2           rprojroot_2.0.3     
#> [76] desc_1.4.1           stringi_1.7.6        parallel_4.1.2       Rcpp_1.0.8.3         vctrs_0.4.2         
#> [81] batchtools_0.9.17    tidyselect_1.1.1     xfun_0.29